[DSP] W01 - Complex Exponential

oscillations

• oscillations are everywhere
• sustainable dynamic systems are always oscillatory
• things that don’t move in circles don’t last
  • bombs
  • rockets
  • human beings (only partially oscillatory)

clip: gyroscopic stability of a disc player in zero-gravity - OFF vs. ON

• an oscillation is cyclic, it goes around in circles
  • all oscillations can be described with a combination of cosine and sine functions

representing an oscillation

• a complex reference system centered on the origin of the oscillation is used for this
• a complex exponential is used to describe the position on the plane of oscillation
• $x\left(t\right)=\exp \left(j\omega t\right)$, where $\exp \left(j\omega t\right)$ is the complex exponential
  • $j=\sqrt{-1}$
  • $\omega$: rotation/oscillation frequency
  • $t$: physical domain time

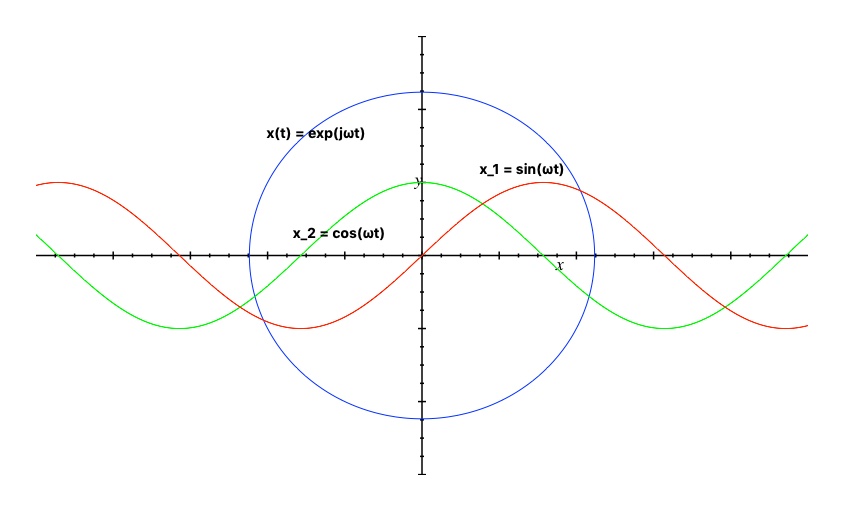
fig: complex exponential in complex plane with sin and cos functions

• trigonometric expansion of complex exponential:
  • $x\left(t\right)=\exp \left(j\omega t\right)=\cos \left(\omega t\right)+j\sin \left(\omega t\right)$
  • called euler’s formula

sample notation with complex exponential

• $x\left[n\right]$: discretized sample notation
• complex exponential sample notation
  • $x\left[n\right]=A\exp \left(j\right(\omega n+\varphi \left)\right)$
• trigonometric complex sample notation
  • $x\left[n\right]=A\left[\cos \right(\omega n+\varphi )+j\sin (\omega n+\varphi \left)\right]$
• where:
  • $\omega$: frequency (radians)
  • $\varphi$: initial phase (radians)
  • $A$: amplitude
• note that phase and frequency are both in radians when using the complex exponential paradigm

---

complex exponential notation

justification for use in dsp

• every sinusoid can be written as a sum of the sine and cosine
  • sine and cosine live together
• trigonometry becomes algebra, so notation is simpler
  • helps avoiding the use of trigonometric identities
    • significantly reduces the number of terms in equations
  • phase can be managed with exponent summation and split rule
  • phase shifts are simple complex multiplications
• complex numbers can be used in digital systems without obstacles

anatomy of the complex exponential

• polar form of complex exponential:
  • $e^{j\alpha }=\cos \alpha +j\sin \alpha$

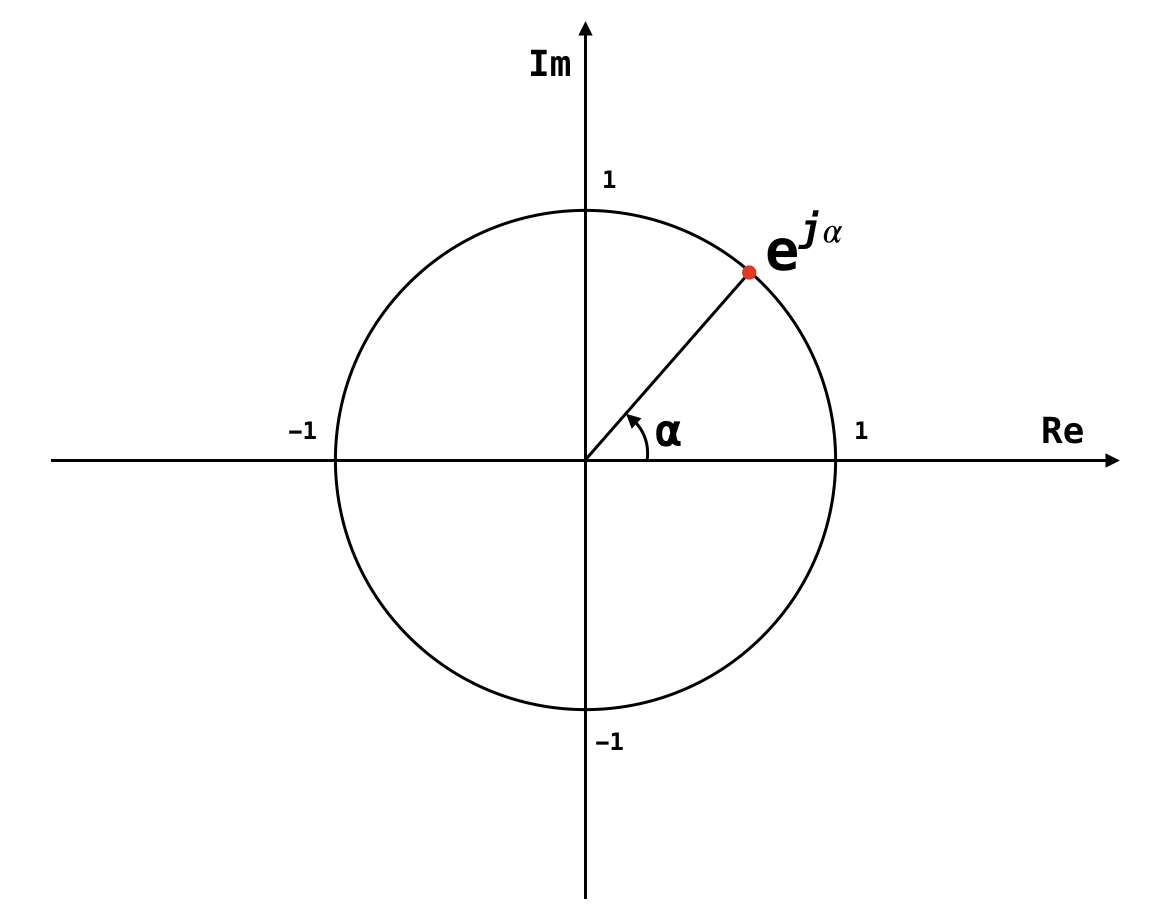
fig: $e^{j\alpha }$ on the complex plane (argand diagram)

• $e^{j\alpha }$ is a unit circle on the complex plane
  • unit circle: $\left|e^{j\alpha }\right|=1$

rotation about the origin complex plane

• say $z$ is a point on the complex plane
  • by multiplying it with $e^{j\alpha }$
  • $z$ is rotated about the origin
    • in the anti-clockwise direction by amount $\alpha$
    • about the origin
    • with radius of rotation $=\left|z\right|$

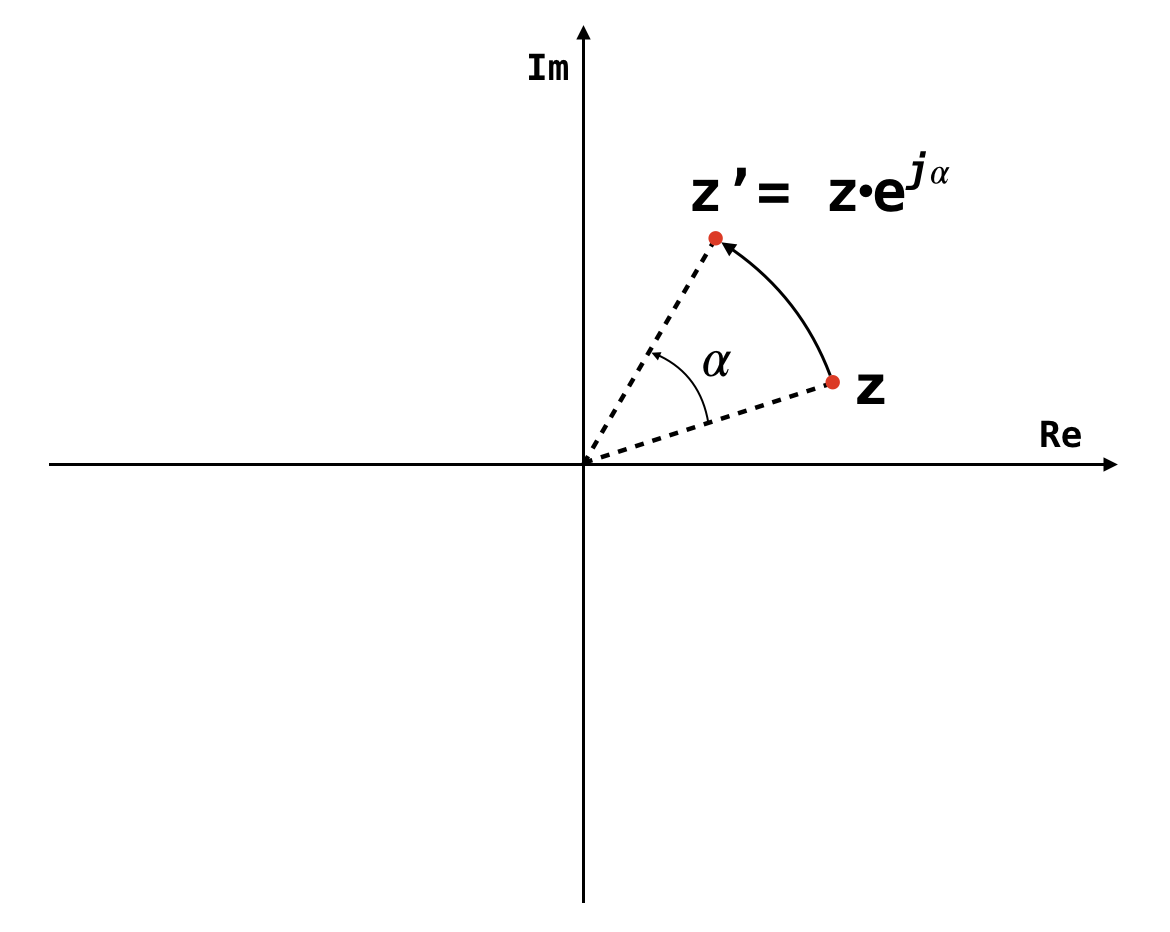
fig: rotation by multiplication with $e^{j\alpha }$

• this rotation operation is the basis of the complex exponential generating algorithm
  • used to synthesize signals
    • $x\left[n\right]=e^{j\omega }$
    • $x[n+1]=e^{j\omega }x\left[n\right]$
    • $x\left[0\right]=1$
  • with an initial phase:
    • $x\left[n\right]=e^{j\omega +\varphi }$
    • $x[n+1]=e^{j\omega }x\left[n\right]$
    • $x\left[0\right]=e^{j\varphi }$
• in discrete time, a sinusoid $e^{j\omega n}$ is periodic only if:
  • $\omega =\frac{M}{N}2\pi$; $M,N\in N$
  • i.e. only if:
    • frequency, $\omega$, is a rational multiple of $2\pi$
    • or equivalently, if $e^{j\omega N}=1$
  • so not every sinusoid is periodic in discrete time

aliasing

• the same point in the unit circle may have many names:
  • the point at $e^{j\alpha }$ can
    • $e^{2\pi +j\alpha }$
    • $e^{6\pi +j\alpha }$
    • $e^{-2\pi +j\alpha }$
• this is called aliasing
  • natural property of complex exponential

• in discrete time, this limits how fast we can go around the unit circle with a discrete-time signal

• the frequency of the discrete-time machine is limited
  • $0\le \omega <2\pi$
  • when it is faster than $2\pi$, due to the periodicity of the complex exponential,
    • we fall back via a modulo operation
• even within the range, care must be taken between backwards and forwards motion
  • when $\omega =\pi$,
    • the point simply oscillates between $1$ and $-1$ on the unit circle
  • when $\omega >\pi$
    • it can also be view as rotation backwards to get that point
    • it is shorter to get to that point in the backwards direction
  • so anytime $\omega >\pi$,
    • it appears like a smaller step in the clockwise direction
  • this reverse effect aliasing is even more pronounced when $\omega$ is close to $2\pi$
  • if $\omega »\pi$, the rotating body appears stationary due to aliasing
• so at different frequencies, i.e. $\omega$ values, aliasing introduces different artifacts of illusion

---

eigenvalues and eigenvectors

• almost all vectors change direction when they are multiplied by a matrix
• however, certain vectors are in the same direction even after multiplication with that matrix
  • those certain vectors are eigenvectors
• since they are the in the same direction, multiplication with the matrix is like scaling the original vector
  • the equivalent scaling factors are called eigenvalues
• consider equation: $Ax=\lambda x$
  • $A$: square matrix
  • $\lambda$: eigenvalues of $A$
  • $x$: eigenvectors of $A$
• rearranging this, we get: $A-\lambda I=0$
  • from this we get A’s characteristic equation:
    • $|A-\lambda I|=0$
    • where $\left|A\right|$: determinant of matrix $A$
  • the roots of this equation are eigenvalues $\lambda$

• having computed the eigenvalues $\lambda$, the eigenvectors $x$ can be found using $Ax=\lambda x$

• if eigenvector elements can take on arbitrary values based on a relationship between them, make sure to normalize them with the square root of the sum of squares of all elements
  • i.e. normalize it with the length (first modulus) of the vector

---

references

• $e^x$ vs. $\exp \left(x\right)$
• argand diagram