[DSP] W03 - Discrete Fourier Transform

contents

• fourier basis
• basis expansion
• DFT calculations
• interpreting a dft plot
• dft in practice

---

fourier basis

• for \(\mathbb{C}^N\)

• in signal notation:
  • \(w_k[n] = e^{j\frac{2\pi}{N}nk}\), for \( n,k = 0,1,\ldots,N-1 \)
• in vector notation
  • \( \{ \textbf{w}^{(k)}\}_{k = 0,1,\ldots,N-1} \)
  • with \( w_n^{(k)} = e^{j\frac{2\pi}{N}nk}\)
• Fourier Basis are a set of N orthogonal vectors
  • hence are a basis for \(\mathbb{C}^N\)
• they are not orthonormal, normalization factor is \( \frac{1}{\sqrt{N}} \)
• will keep normalization factor explicit in DFT formulas

---

basis expansion

analysis formula

• \( X_k = \langle \textbf{w}^{(k)}, x \rangle \)

synthesis formula

• \( x = \frac{1}{N}\sum_{k=0}^{N-1}X_k\textbf{w}^{(k)} \)

change of basis in matrix form

• analysis formula:
  • \( \textbf{X} = \textbf{W}\textbf{x} \)
• synthesis formula:
  • \( x = \frac{1}{N}\textbf{W}^H\textbf{X} \)

signal notation

• analysis formula:
  • \( X[k] = \sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}nk} \)
    • \( k = 0,1,\ldots,N-1 \)
    • N point signal in the frequency domain
• synthesis formula:
  • \( x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j\frac{2\pi}{N}nk} \)
    • \( n = 0,1,\ldots, N-1 \)
    • N point signal in time-index domain for discrete time

---

DFT calculations

dft is linear

• \( DFT \{ \alpha x[n] + \beta y[n] \} = \alpha DFT \{ x[n] \} + \beta DFT \{ y[n] \} \)

dft of \( \delta[n] \)

• here: \(x[n] == \delta[n] \)
• \( X[k] = \sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}nk} \)
  • \( \sum_{n=0}^{N-1}\delta[n]e^{-j\frac{2\pi}{N}nk} = 1\)

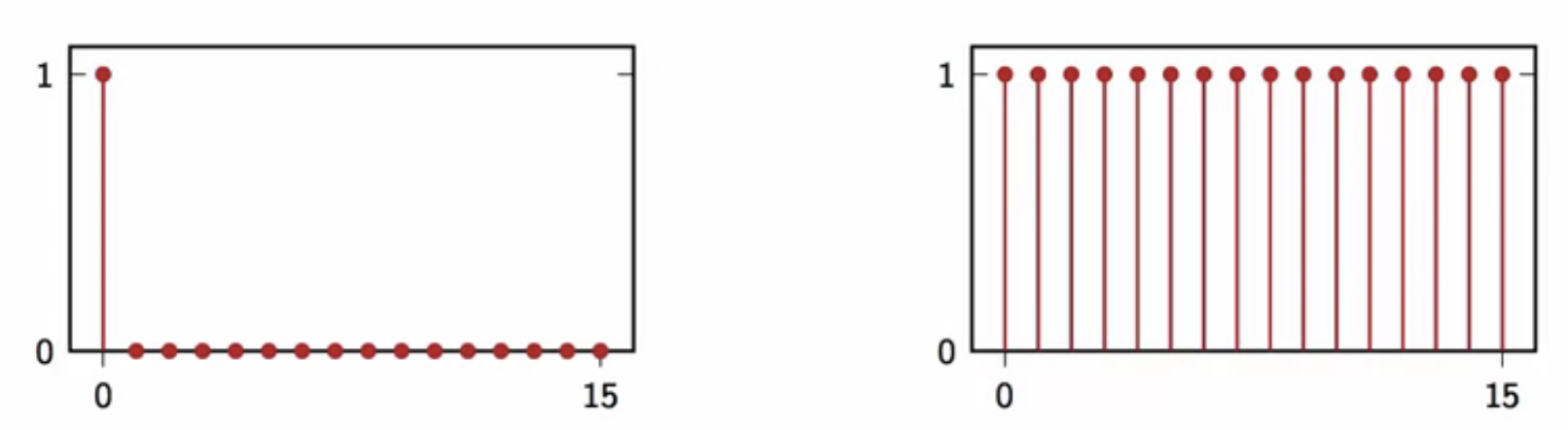
fig: fourier transform of discrete-time delta

dft of \( x[n] = 1 \)

• for \( x[n] \in \mathbb{C}^N\)

• \( X[k] = \sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}nk} \)

  • \( \sum_{n=0}^{N-1}e^{-j\frac{2\pi}{N}nk}\)
  • \( N\delta[k] \)

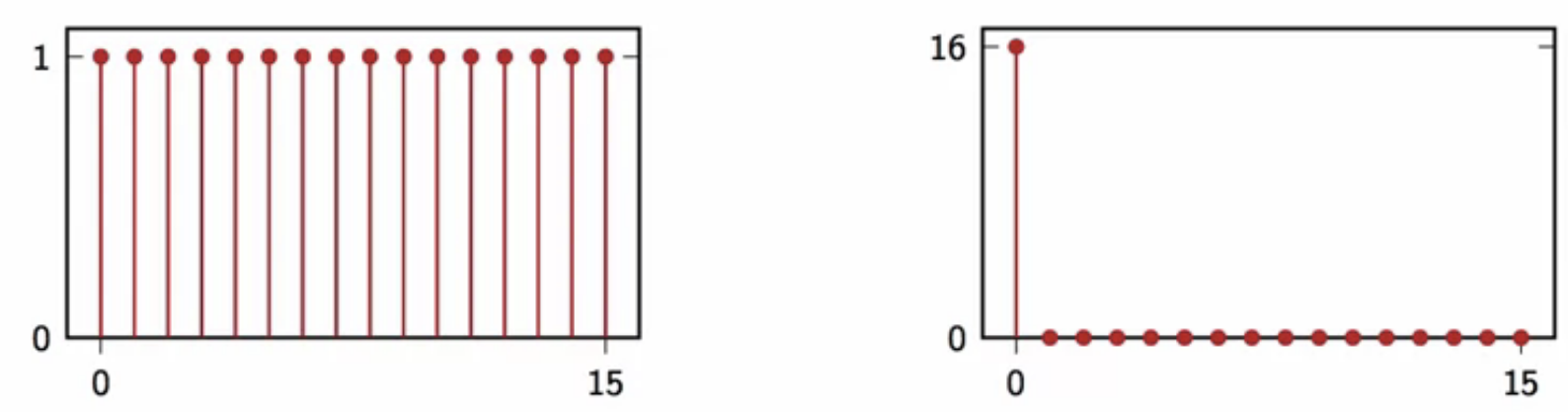
fig: fourier transform of function 1

dft of \( x[n] = 3 \cos{\frac{2\pi n}{16}} \)

• for \( x[n] \in \mathbb{C}^{64}\)

• in \( \mathbb{C}^{64} \), the fundamental frequency of the fourier transform is \( \omega = \frac{2\pi}{64} \)

• \( x[n] = 3 \cos{\frac{2\pi n}{16}} \)
  • \( = 3 \cos{\frac{4 (2\pi) n}{64}} \)
  • use expansion: \( \cos \omega = \frac{ e^{j\omega} + e^{-j\omega} }{2} \)
  • \( = \frac{3}{2}\Big[ e^{j\frac{2\pi}{64} (4n)} + e^{-j \frac{2\pi}{64} (4n)} \Big] = \frac{3}{2}\Big[ e^{j\frac{2\pi}{64} (4n)} + e^{j \frac{2\pi}{64} (60n)} \Big] \)
  • \( = \frac{3}{2}\Big( w_4[n] + w_{60}[n] \Big) \)
• so \( X[k] = \langle w_k[n],x[n] \rangle \)
  • \( = \langle w_k[n], \frac{3}{2}(w_4[n] + w_{60}[n]) \rangle \)
  • \( = \frac{3}{2} \langle w_k[n], w_4[n] \rangle + \frac{3}{2} \langle w_k[n] + w_{60}[n]) \rangle \)
  • \( = \bigg \{ \begin{matrix} 96 & for \text{ } k = 4,60 \\ 0 & otherwise \end{matrix} \)

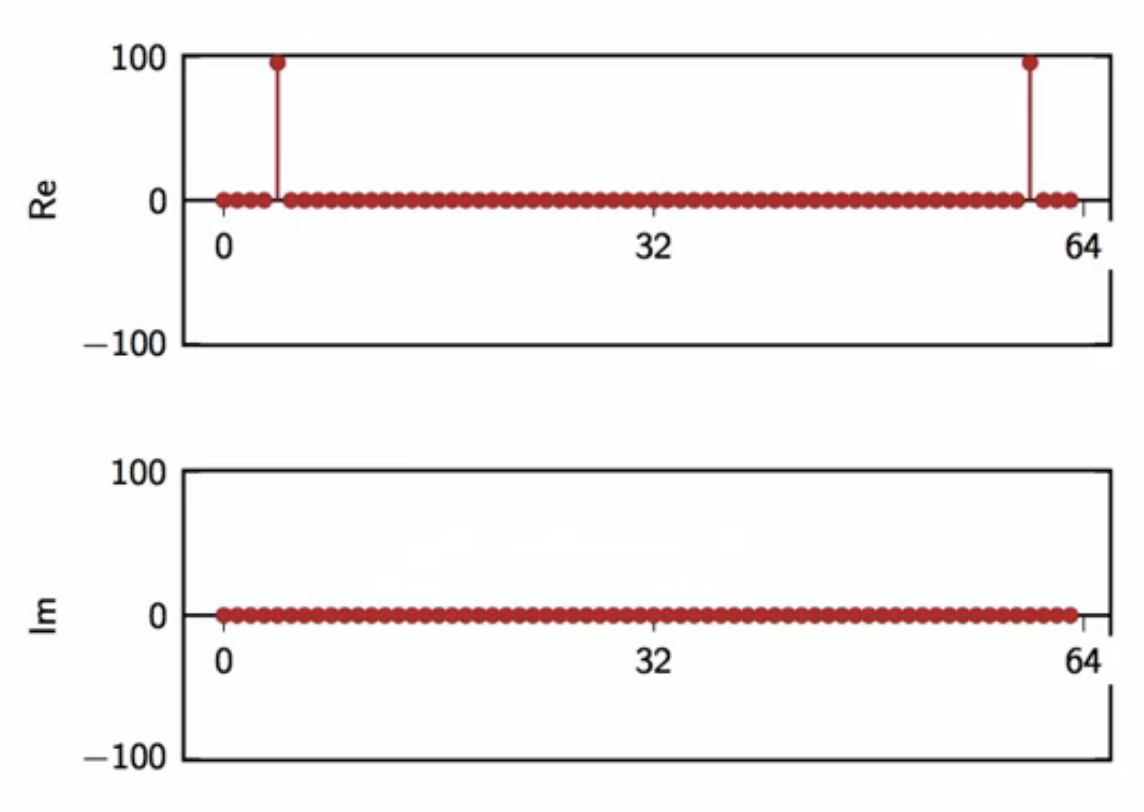
fig: [Re] and [Im] of DFT of \( x[n] = 3 \cos{\frac{2\pi n}{16}} \)

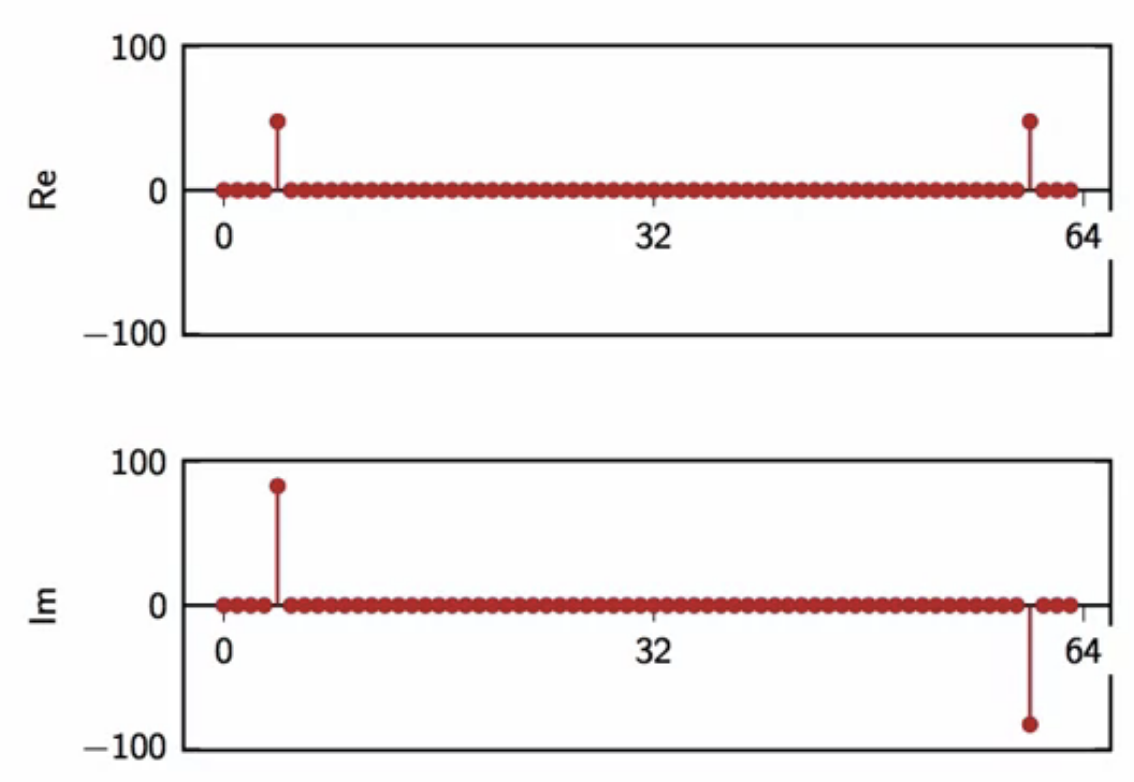
fig: similarly, [Re] and [Im] of DFT of \( x[n] = 3 \cos{\frac{2\pi n}{16} + \frac{\pi}{3}} \)

---

interpreting a dft plot

rotation direction

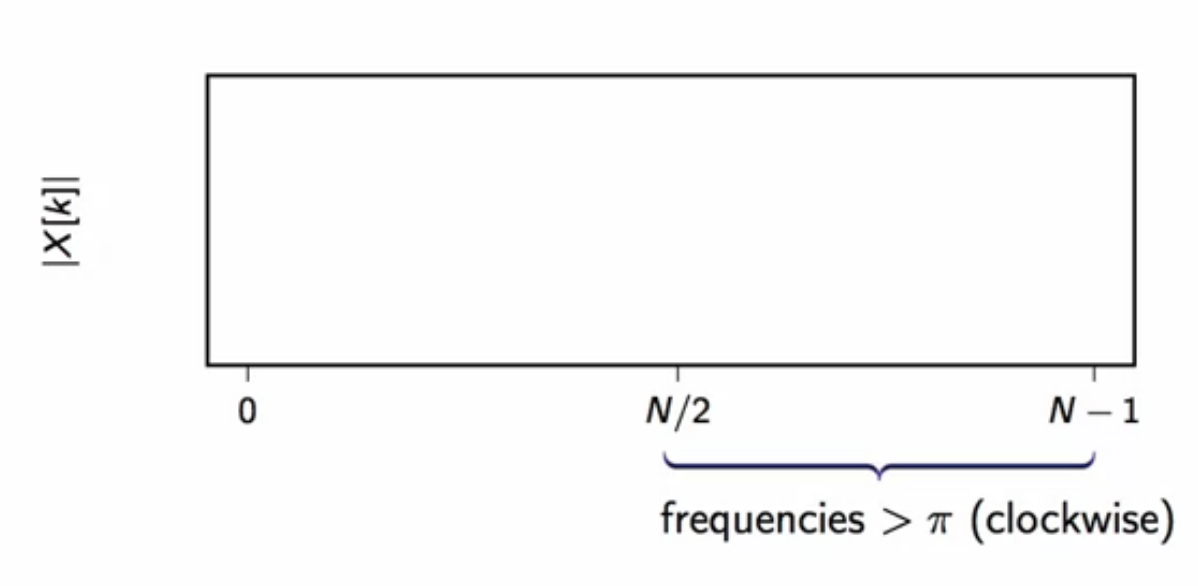
fig: dft chart frequency rotation

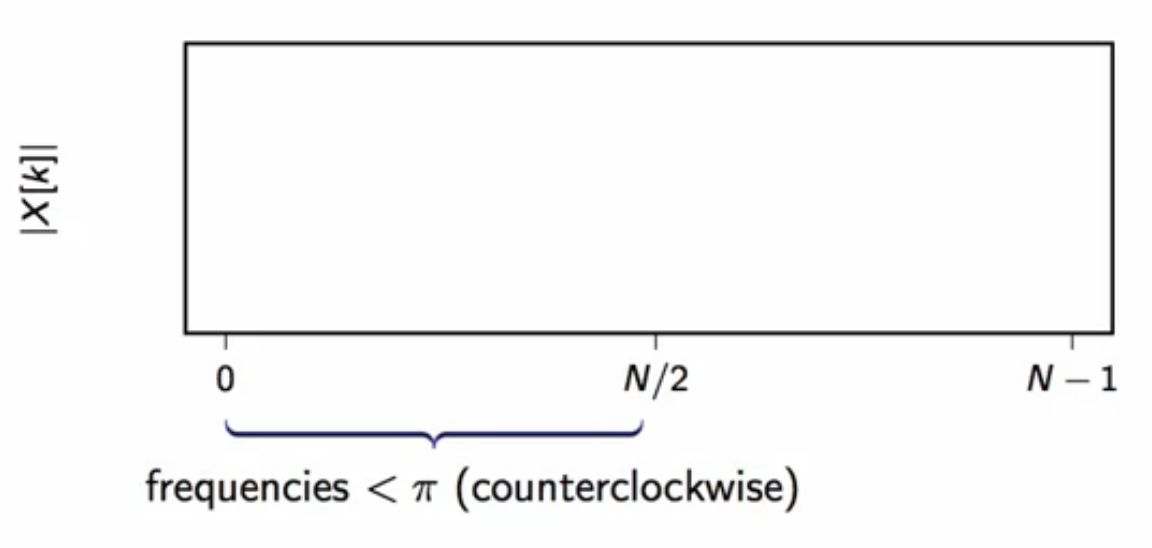
fig: dft chart frequency rotation

speed distribution

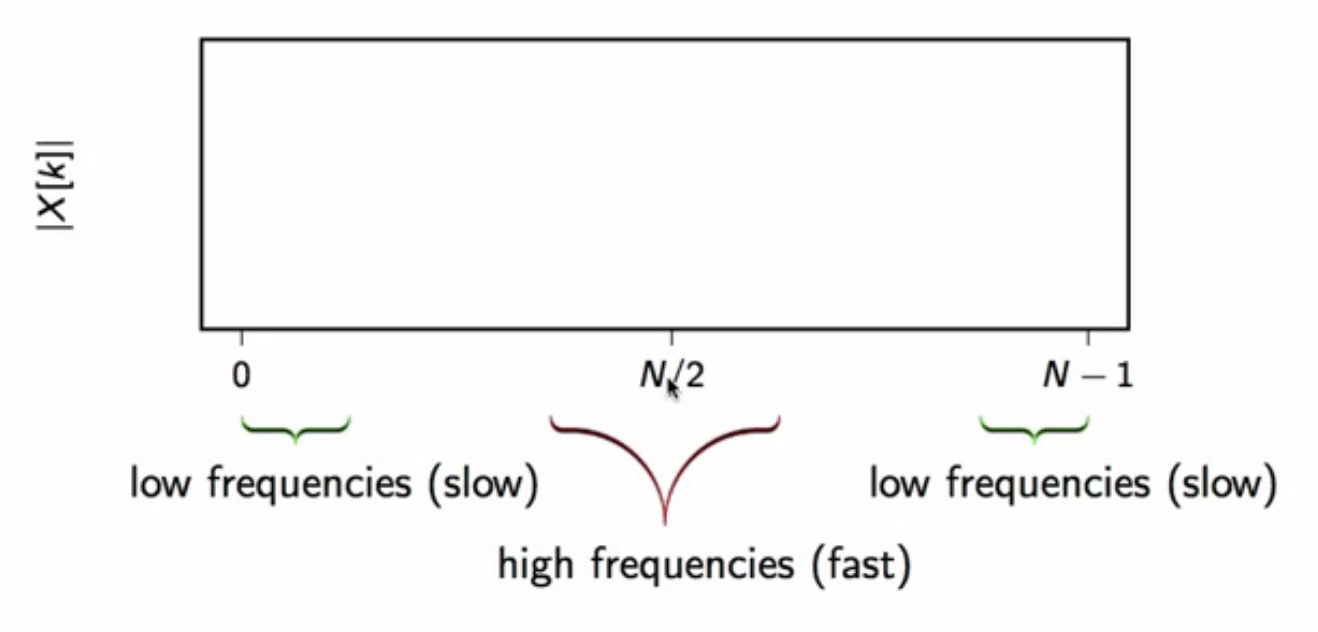
fig: dft chart frequency distribution

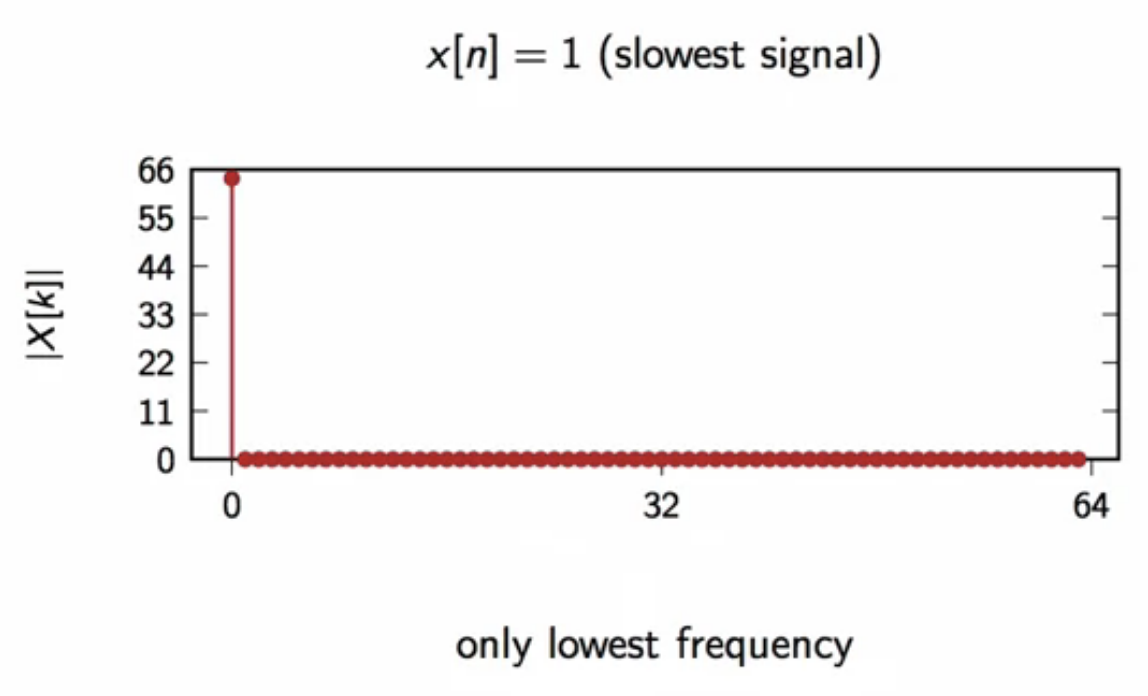
fig: stationary frequency (k=0)

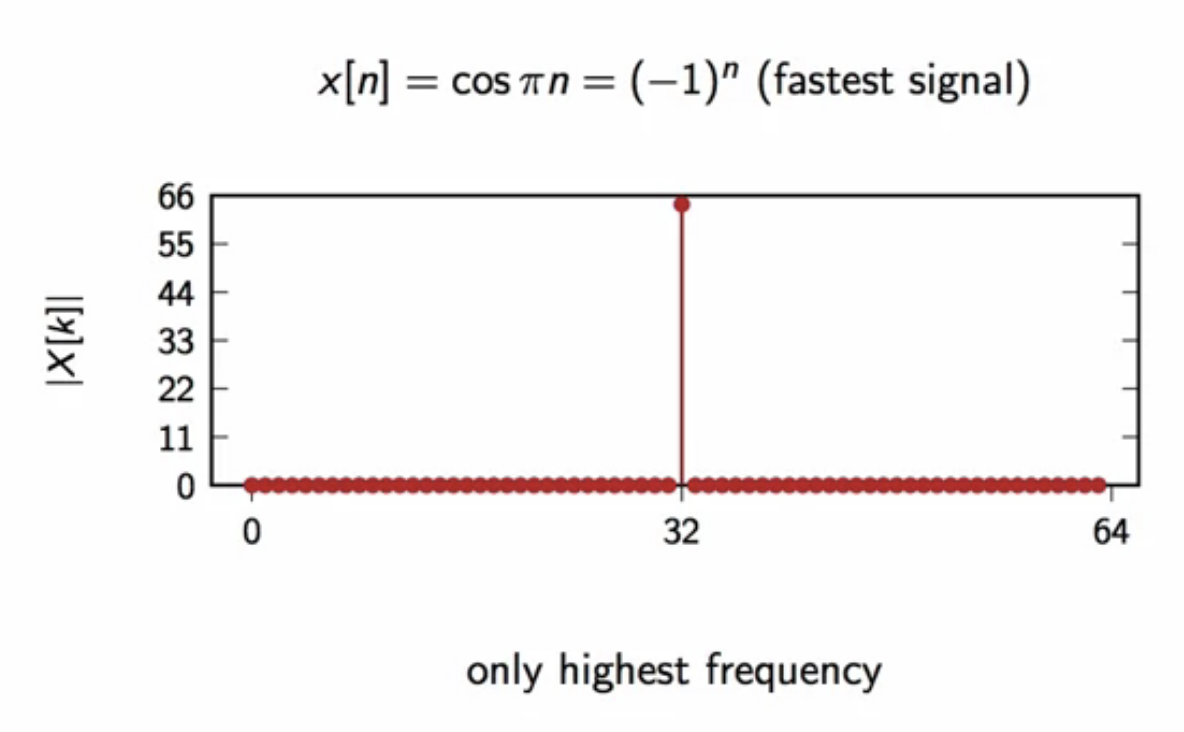
fig: fastest frequency (k=32)

energy distribution

• Conservation of Energy across domains:
  • underlying energy of a signal doesn’t change with change of basis
• Square magnitude of k-th DFT coefficient proportional to signal’s energy at frequency \( \omega = \frac{2\pi}{N}k\)

dft of real signals

• dft of real signals are symmetric in magnitude

---

dft in practice

• the highest frequency of a digital system is half of the inherent sampling rate
  • \(f_{max} = \frac{F_s}{2}\)
• in the DFT window, this corresponds to the mid-point of the window
  • i.e. \( k = \frac{N}{2} \)
• so first find \( k = \frac{N}{2} \), and set that equal to half the sampling frequency
• then, use linear interpolation to find that smaller components’ frequencies
  • \( f_s = \frac{\frac{F_s}{2}k}{\frac{N}{2}} \)

fourier analysis of musical instruments

• the played note is the first peak: 220Hz for example
  • this is the pitch of the instrument
• the other peaks are called harmonics, they define the typical sound of the instrument

short-time fourier transform (STFT)

• dual-tone multi frequency (dtmf dial phone)

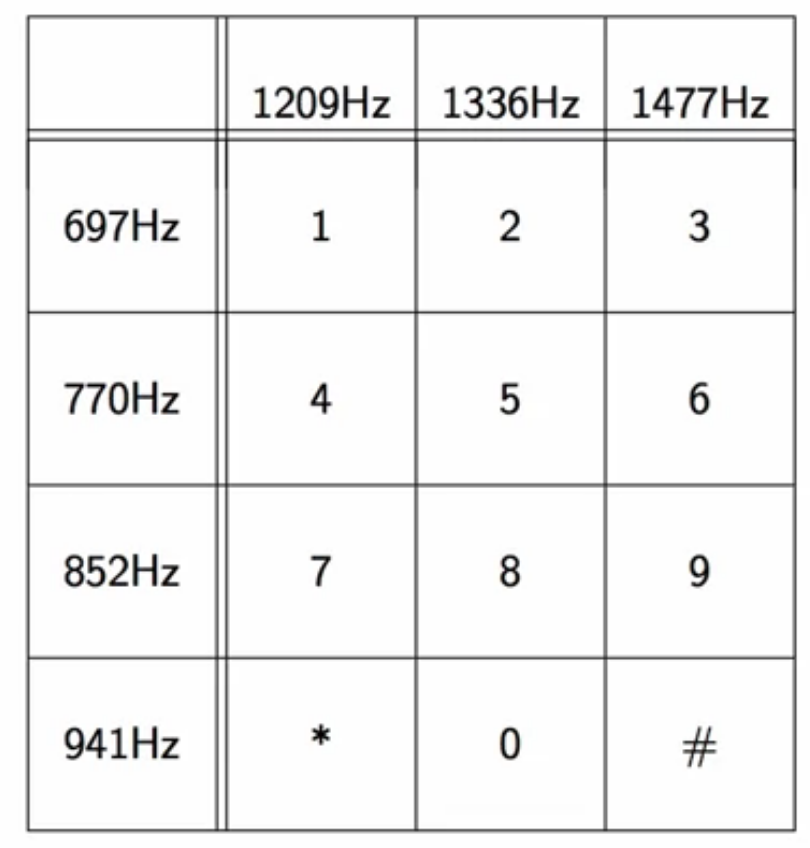
fig: dtmf dial-pad

• when say key 4 is pressed,
  • two sinusoids are generated, one specified at the row and another by the column
  • 770 Hz and 1209 Hz
• the frequencies are chosen such that they are co-prime
• no sum or differences in frequencies are the same as the any of the chosen frequencies

• goal is to minimized errors while decoding pressed numbers at the exchange

• fundamental trade-off in signals
  • time representation obfuscates frequency information
  • frequency representation obfuscates time
• so, the signal at the exchange is subjected to DFT in small chucks of window
  • each window is applied to the burst of sound corresponding to a key press
• so, in that way STFT is just standard DFT applied to a restricted portion of a signal
• it is useful to obtain simultaneously obtain time and frequency information

the spectrogram

• color-code the magnitude
  • dark is small
  • white is large
• use \( 10 \text{ } log_{10}(\vert X[m;k]\vert) \) to see better (power in dBs)
  • plot spectral slices one after another
• spectrogram can be applied to visualize the numbers dialled using a DTMF dialpad

• spectrogram can be wide-band or narrow-band, based on the number of points samples

• in a long window, more frequency resolution can be had
  • but since it is sensitive to a lot of things happening over time, it is not precise in time
• in a short window, many time slices - precise location of transitions
  • short window, fewer DFT points - poor frequency resolution
• to better localize the position of a start and end of a key press, the length of the DFT has to be reduced

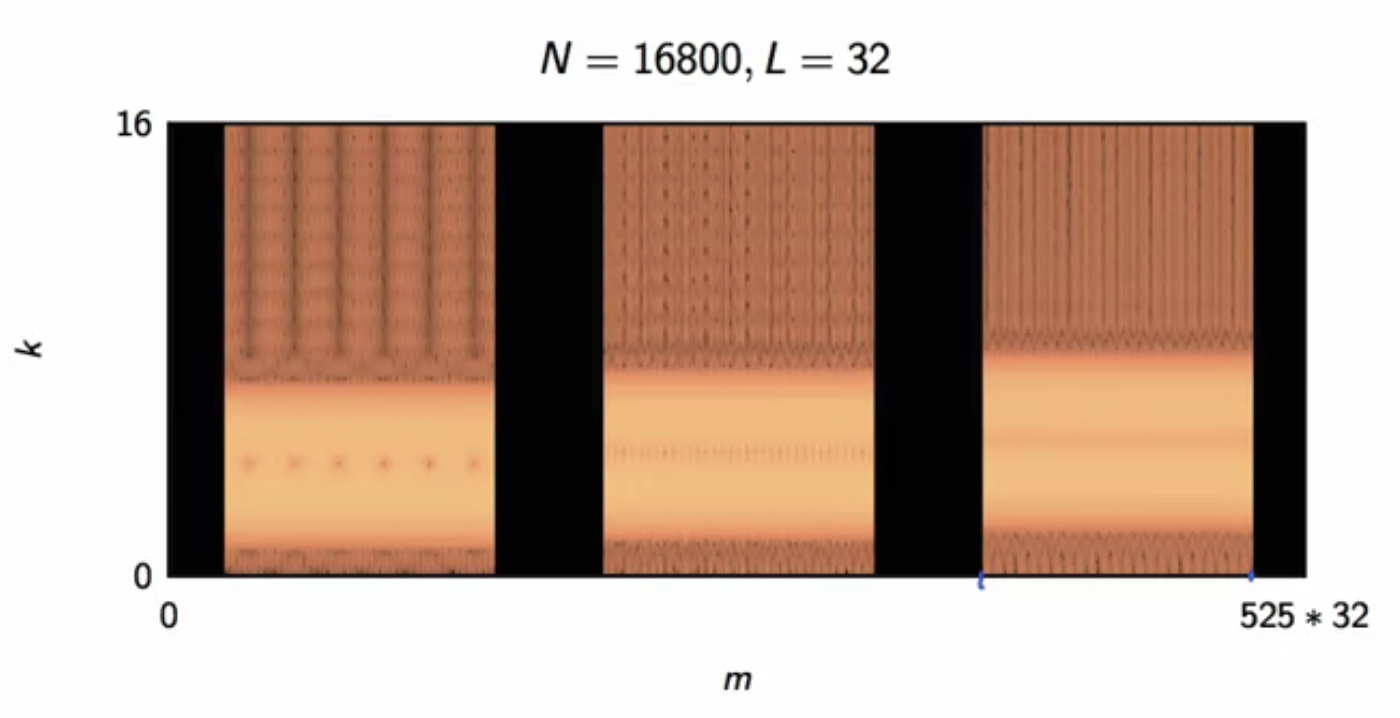
fig: dtmf dial-pad wideband spectrogram

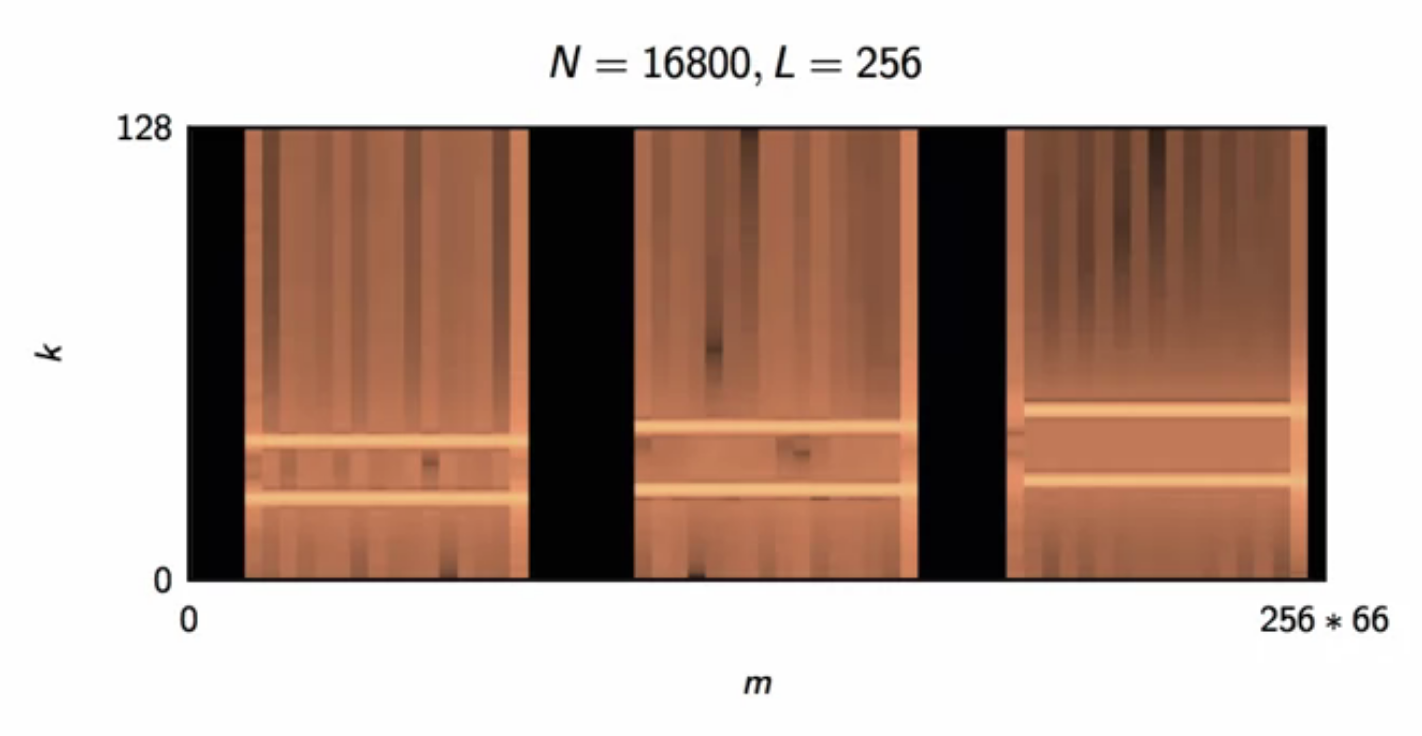
fig: dtmf dial-pad medium band spectrogram

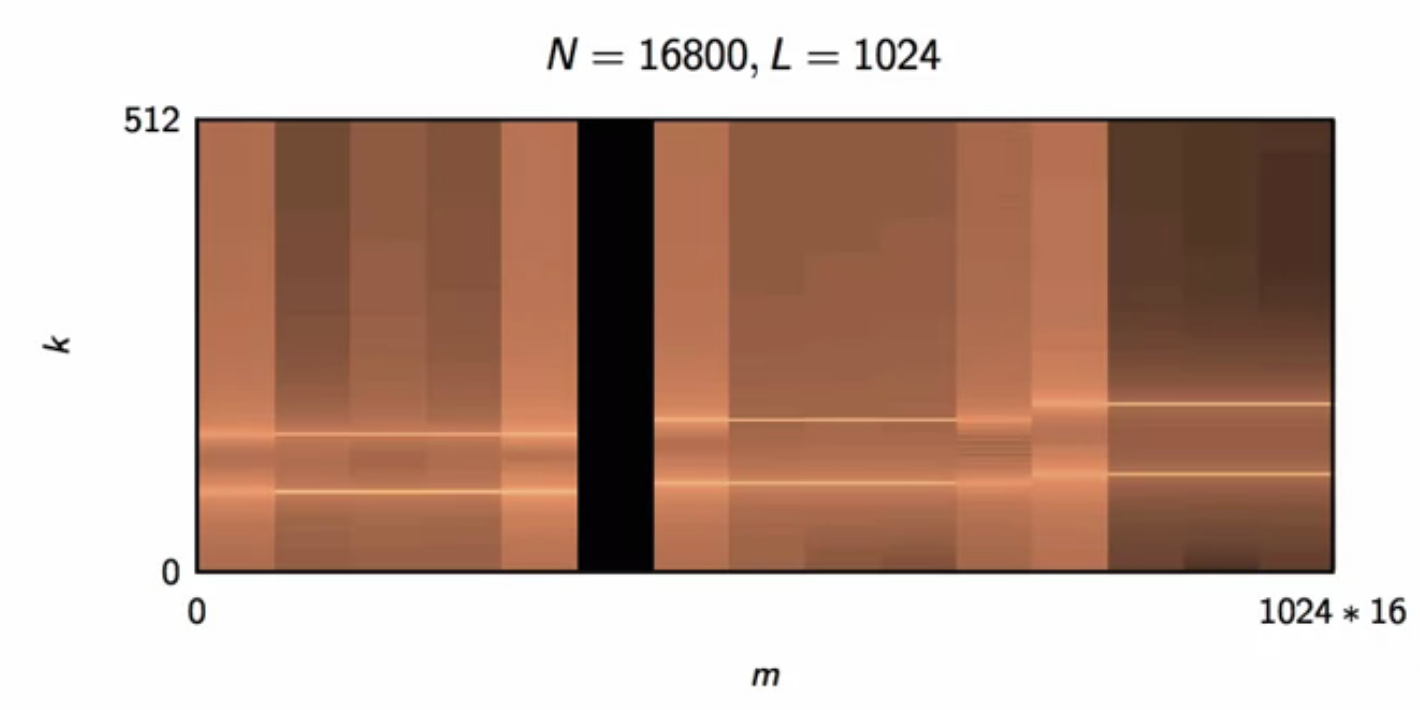
fig: dtmf dial-pad super narrow band spectrogram

---

references

• coursera dsp