contents

signal processing

  • signal processing is where a signal is manipulated to transform it into another signal after analysis
  • there are many ways to skin a signal

filters

  • this post is focussed on linear time-invariant filters
    • LTI filters
  • these are simple, yet powerful devices that have been around a long time i.e. since analog electronics have existed
  • example:
    • boosting bass on stereo system
    • dim treble on stereo system
  • in the digital signal world, the implementation of these filters is simpler on general purpose architecture
  • goals:
    • define the filter paradigm
      • filter characterization
      • ideal filters
    • implementing filters
    • filter design (and beyond ideal filters)
      • z-transform in filter design
  • this covers the very basics of filters in dsp

linear filters

  • SISO: a single-input-single-output signal processor takes in a single input, operates on it and outputs the resulting signal fig: dsp SISO block
    • (x[n]): input signal
    • (y[n]): output signal
    • ( \mathcal{H} ): operator block
    • where: ( y[n] = \mathcal{H}{ x[n] } )
  • this operation (\mathcal{H} ) can be anything and is limitless -so operation modified as per dsp application
  • for a filter, this operation has some restrictions fig: LTI SISO filter requirements

linearity

  • operation on sum of two signals must result in the same as the sum of operation result separately on the two signals \[ \mathcal{H} { \alpha x_1[n] + \beta x_2[n] } = \alpha \mathcal{H} { x_1[n] } + \beta \mathcal{H} { x_1[n] } ]
  • addition and scalar multiplication are covered under linearity

time-invariance

  • the operator result for a given signal must be same whenever it is applied, independent of time \[ y[n] = \mathcal{H} { x[n] } \Leftrightarrow \mathcal{H} { x[n - n_0] } = y[n - n_0] ]

causal system

  • this is an optional requirement
    • helps real-time LTI system implementation
  • system depends only on the input and output values of the past
    • along with present input
  • physical or non-anticipatory system \[ y[n] = \mathcal{H}( x[n], x[n-1], x[n-2], \ldots, y[n-1], y[n-2], \ldots ) ]
    • here: ( \mathcal{H}(\cdot) ) is a linear function of its arguments

impulse response

  • impulse response of filter (h[n]):
    • the output of a filter when the input is ( \delta )
    • ( h[n] = \mathcal{H}{\delta[n]})
  • impulse response fully characterizes the behavior of an LTI system
    • this is because all arbitrary inputs can be expressed in terms of a (\delta) signal
  • so, knowing the response of a filter to the delta signal, along with linearity conditions, filter response for any arbitrary signal can be computed

example

  • consider filter characterized by ( h[n] = \alpha^n u[n] ) : fig: impulse response ( h[n] = \alpha^n u[n] )
  • here ( h[n] = \mathcal{H} { \delta[n]} )
  • an arbitrary signal is fed to the filter: fig: arbitrary input signal to filter whose ( h[n] ) is known
  • all signals can be represented in terms of the ( \delta ) function \[ x[n] = \sum_{k=-\infty}^{\infty} x[k] \delta[n-k] ]
  • since all signals can be represented in terms of the ( \delta ) function, above input signal is cast in terms of the (\delta ) signal to obtain

\[ x[n] = 2\delta[n] + 3\delta[n-1] + \delta[n-2] ]

  • to compute the output ( y[n] ) of the filter for the above input \[ \begin{align} y[n] & = \mathcal{H} { x[n] }
    & = \mathcal{H} { 2\delta[n] + 3\delta[n-1] + \delta[n-2] }
    & = \mathcal{H} { 2\delta[n] } + \mathcal{H} { 3\delta[n-1] } + \mathcal{H} { \delta[n-2] }
    & = 2 \mathcal{H} { \delta[n] } + 3 \mathcal{H} { \delta[n-1] } + \mathcal{H} { \delta[n-2] }
    & = 2 h[n] + 3 h[n-1] + h[n-2]
    \end{align} ]

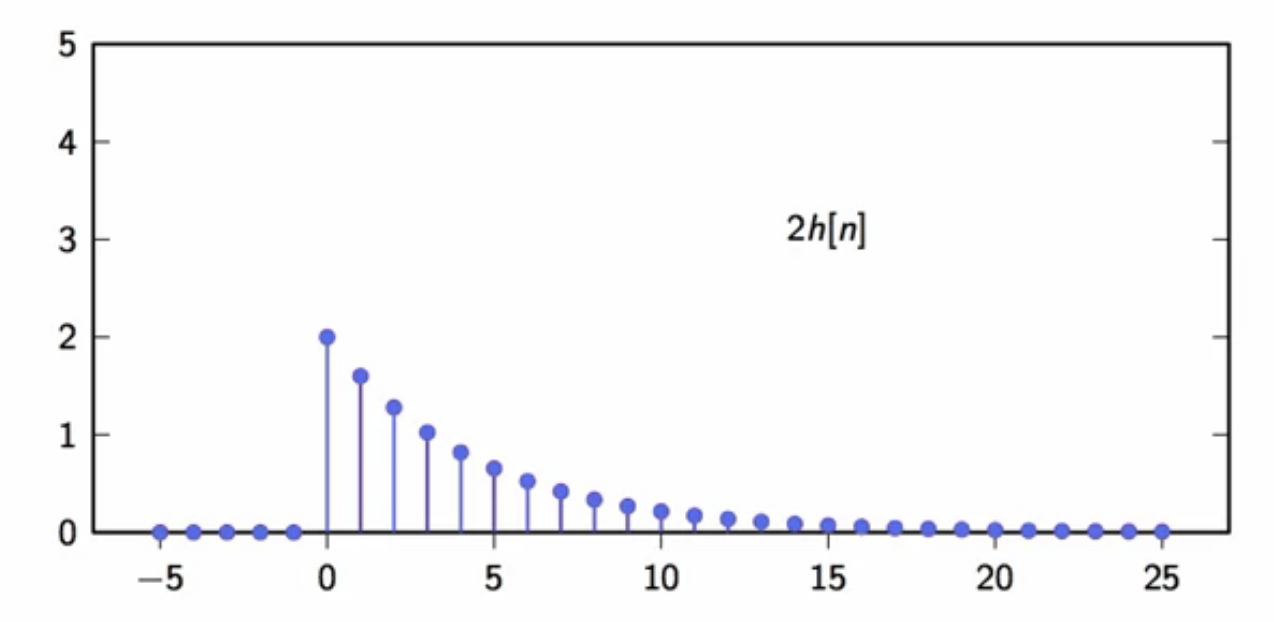
imp-res-02

fig: first filter output component ( 2 h[n] )

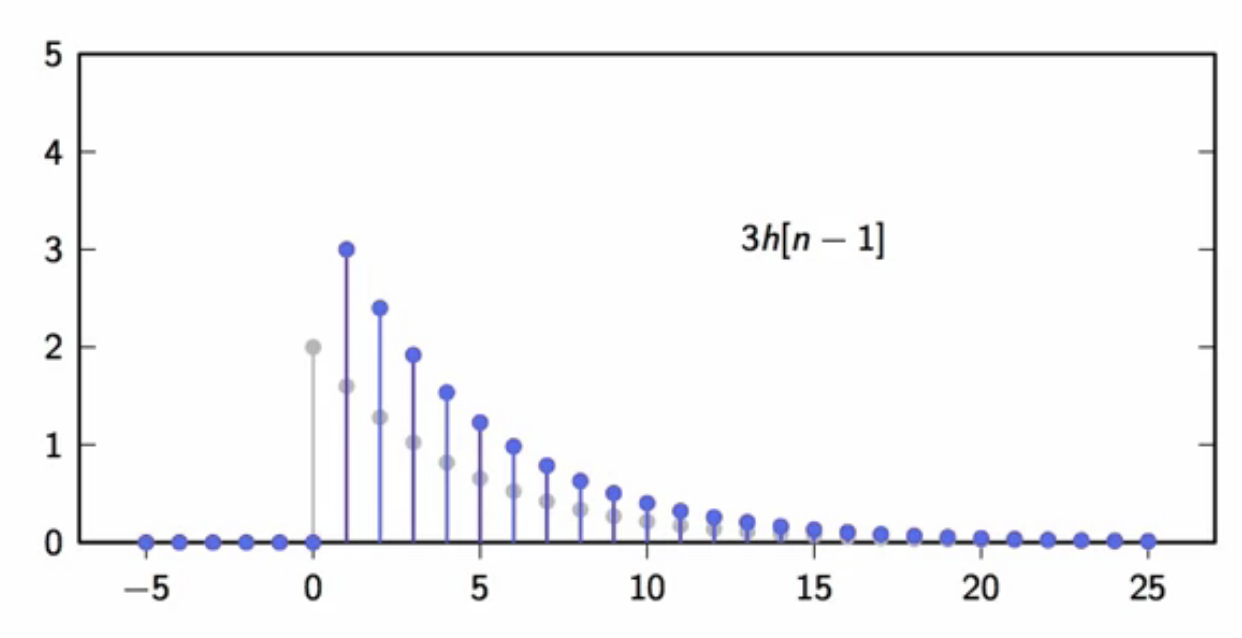
imp-res-03

fig: second filter output component ( 3 h[n-1] )

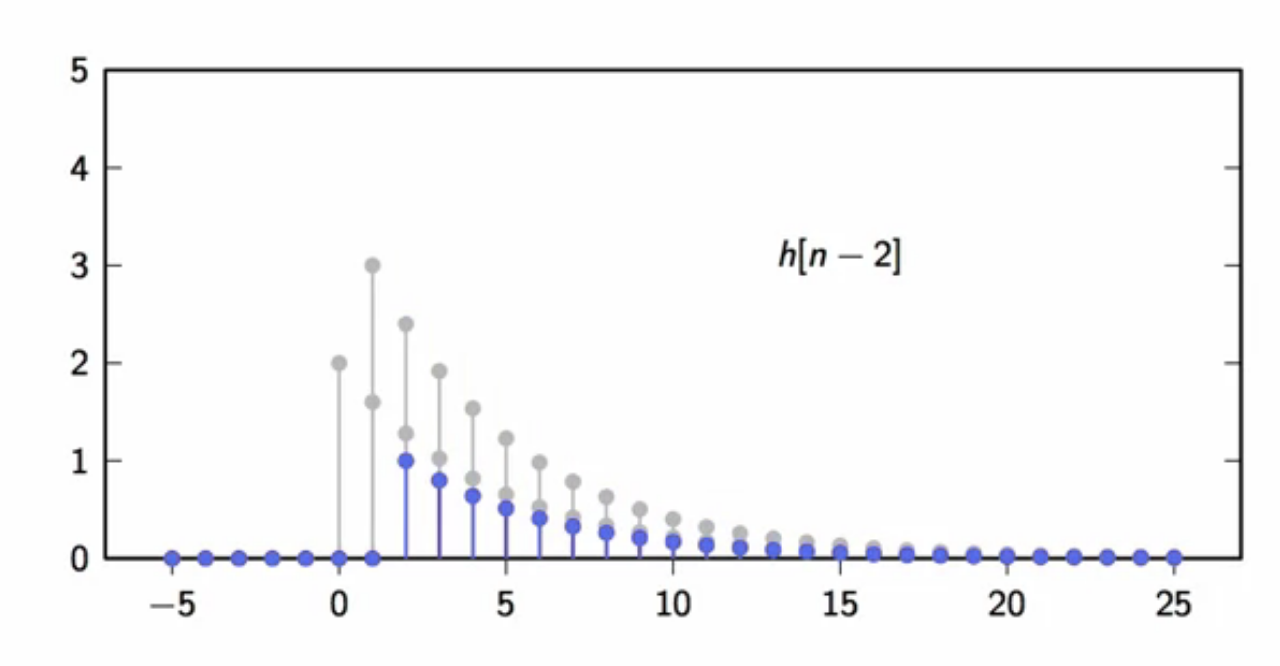
imp-res-04

fig: third filter output component ( h[n-2] )

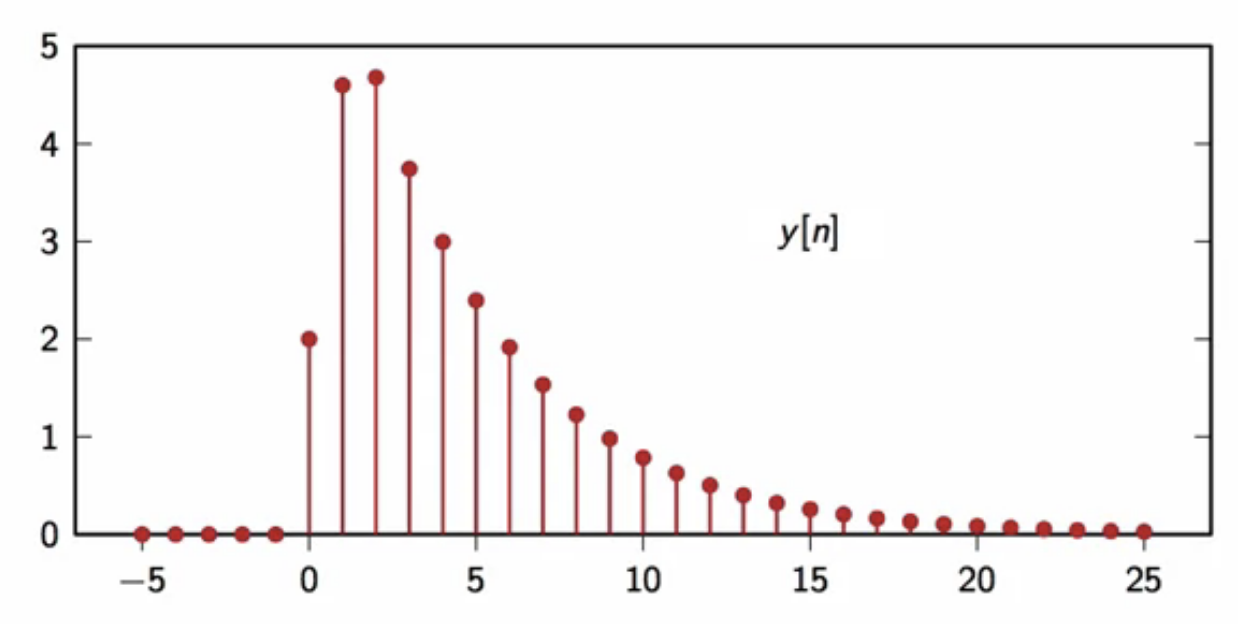
imp-res-05

fig: sum of components of filter output ( y[n] )

  • so, output of a filter for any arbitrary signal can be expressed in terms of the impulse response (h[n]) \[ \begin{align} y[n] & = \sum_{k = -\infty}^{\infty} x[k] h[n-k]
    y[n] & = x[n] * h[n] \end{align} ]
  • above filter operation is called convolution

convolution

\[ \begin{align} x[n] * h[n] & = \sum_{k = -\infty}^{\infty} x[k] h[n-k]
\end{align} ]

inputs of convolution:

  • a sequence: (x[m] )
  • a second sequence: ( h[m] )

convolution procedure:

  • time-reversed: ( h[m] )
  • at each step (n) (from (-\infty ) to (\infty))
    • center the time-reversed ( h[m] ) in ( n )
      • i.e. shift by (-n)
    • compute the inner product of the two signals

convolution properties

  • linearity and time invariance
  • commutativity:
    • ( x[n] _h[n] = (h_n)[n] )
    • filter order doesn’t matter in a cascade of filters, they can be switched
  • associativity: (for absolutely- and square-summable sequences)
    • ( (x h) w)[n] = (x (h w))[n] ) 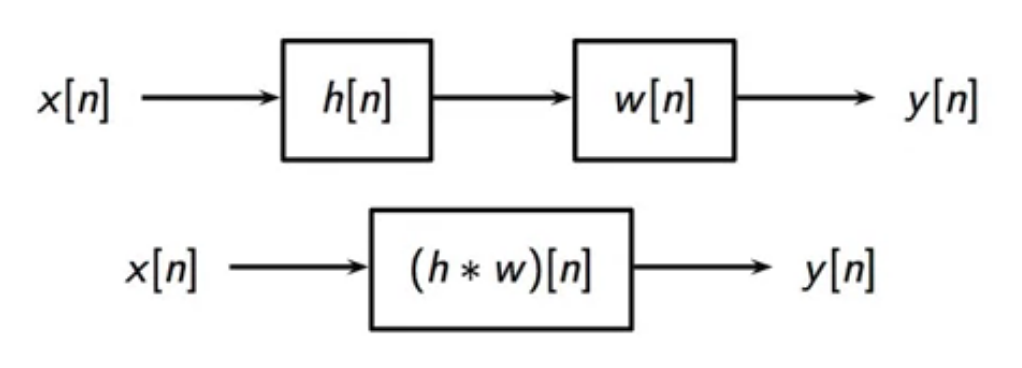imp-res-06 fig: associativity - filters can be lumped in a filter cascade

applications

  • auralization
    • apply room-impulse-response to sounds in virtual reality
    • used in music production to simulate environment effects
  • dry sounds are convolved with room-impulse-responses to create mental imagery in sounds
  • realistic impulses are only approximations to dirac-delta function
    • so the room-impulse-responses convolutions are not perfect
  • shape of an environment can be reproduced in sound
    • if the room is not too complex
    • involves localization of multiple sources
    • multiple sound sensors can localize the room-response better as they can localize more features of the room

filtering applications

  • there are several applications of filtering, noise filtering is one of them
  • consider the scenario where a smooth signal is measured
    • due to the measurement process, the measured value has a perturbation that affects the smoothness of the measured signal
    • this leads to a noisy signal fig: noisy signal resulting from a measurement
  • noise filtering:
    • removing noise from an otherwise smooth signal
    • apply dsp to get as close as possible to the original smooth signal
  • examples of noise filters (de-noising):
    • moving-average
    • leaky integrator

moving-average filter

  • replace each sample of the input sequence by the local average
  • 2-pt moving-average filter: \[ y[n] = x[n] + \frac{x[n-1]}{2} ] fig: measured signal filtered with 2-pt moving-average
  • more general moving-average filter \[ y[n] = \frac{1}{M} \sum_{k=0}^{M-1}x[n - k] ]
<img class="plot mx-auto text-center img-fluid" src="/images/uploads/noise-filter-02.png" alt="nf-02">

*fig: measured signal filtered with 4-pt moving-average*
{: style="font-size: 80%; text-align: center;"}

<img class="plot mx-auto text-center img-fluid" src="/images/uploads/noise-filter-03.png" alt="nf-03">

*fig: measured signal filtered with 12-pt moving-average*
{: style="font-size: 80%; text-align: center;"}

<img class="plot mx-auto text-center img-fluid" src="/images/uploads/noise-filter-04.png" alt="nf-04">

*fig: measured signal filtered with 100-pt moving-average*
{: style="font-size: 80%; text-align: center;"}

- the 100-pt moving-average is very smooth, but the output has a delay with respect to the input
- this is because a large amount of input samples have to accumulated before the average can be computed for a point 
- so delay is the price to pay for more a more smoothed out signal
moving-average - impulse response
  • (M)-pt moving-average filter characterization
    • done with impulse response input \[ \begin{align} h[n] & = \frac{1}{M} \sum_{k=0}^{M-1} \delta [n-k]
      & = \Bigg { \begin{matrix} \frac{1}{M} & \text{ for } 0 \leq n < M \ 0 & \text{ otherwise } \end{matrix}
      \end{align} ] fig: impulse response (h[n]) of (M)-pt moving-average filter
moving-average - analysis
  • proportional to ( M )
    • smoothing effect
    • number of operations for computing each output
    • storage and memory used
    • delay of output w.r.t signal to be smoothed
  • here, while better smoothing is desired, the cost gets in the way
    • so another method is explored to reduce smoothing costs of a signal, while keeping the smoothing effect high

first-order recursion

  • technique to reduce the computation power and memory needed for large-pt moving-average
  • derivation:
    • moving-average of (M) points: \[ \begin{align} y_M[n] & = \frac{1}{M} \big ( x[n] + x[n-1] + x[n-2] + \ldots + x[n - M + 1] \big )
      \end{align} ]
    • rearranging: \[ \begin{align} y_M[n] & = \frac{1}{M} x[n] + \frac{1}{M} \big ( x[n-1] + x[n-2] + \ldots + x[n - M + 1] \big )
      \end{align} ]
    • here, the second term of the sum has ( M-1 ) terms
    • this is similar to the moving-average of (M-1) terms \[ \begin{align} y_{M-1}[n-1] & = \frac{1}{M} \big ( x[n-1] + x[n-2] + \ldots + x[n - M + 1] \big )
      \end{align} ]
      • i.e. moving-average over ( M - 1 ) points, delayed by one
  • formally: [ \begin{align} y_M[n] & = \frac{1}{M} \sum_{k=0}^{M-1} x[n-k]
    y_M[n - 1] & = \frac{1}{M} \sum_{k=1}^{M-1} x[n-k]
    y_{M-1}[n-1] & = \frac{1}{M-1} \sum_{k=1}^{M-1} x[n-k]
    \end{align} ]
    • also, summing only first ( M-1 ) samples: [ \begin{align} \sum_{k=0}^{M-1} x[n-k] = x[n] + \sum_{k=1}^{M-1} x[n-k]
      \end{align} ]
    • comparing it to the above set of equations: [ \begin{align} My_M[n] = x[n] + (M-1)y_{M-1}[n-1]
      \end{align} ]
    • this relates the moving-average between (M ) points ( My_M[n] ) and the moving-average of (M - 1 ) points delayed by 1 (y_{M-1}[n-1])
    • rearranging for (y_{M}[n]): \[ \begin{align} y_M[n] = \frac{1}{M} x[n] + \frac{M-1}{M}y_{M-1}[n-1]
      \end{align} ]
    • introducing ( \lambda = \frac{M-1}{M} ) [ \begin{align} y_M[n] = \lambda y_{M-1}[n-1] + (1-\lambda) x[n]
      \end{align} ]

leaky integrator

  • in a moving-average filter, when (M) is large, assume: \[ \begin{align} y_{M-1}[n-1] & \approx y_M[n]
    \lambda & \approx 1 \end{align} ]
    • i.e. average doesn’t change much by excluding one data point
  • this assumption is applied to the recursive moving-average filter
    • which yields the leaky integrator filter \[ \begin{align} y[n] = \lambda y[n-1] + (1-\lambda) x[n]
      \end{align} ]
  • this filter is recursive:
    • previous output value is used to compute current value
  • de-noising for various (\lambda ) values: fig: measured signal filtered with (\lambda = 0.2) leaky-integrator

    fig: measured signal filtered with (\lambda = 0.5) leaky-integrator

    fig: measured signal filtered with (\lambda = 0.8) leaky-integrator

    fig: measured signal filtered with (\lambda = 0.98) leaky-integrator

leaky integrator - analysis
  • closer the value of (\lambda ) to (1), more the smoothing
  • ( \lambda ) values very close to (1) provides smoothing power similar to a moving-average filter with large (M)
  • so, the leaky integrator is a special case of a moving-average filter
    • for when the (M) values are large
  • each average requires only three operations
    • average at every point is ( y[n] = \lambda y[n-1] + (1-\lambda)x[n] )
    • two multiplications, one addition
  • number of operations are independent of ( \lambda ) value
    • so high smoothing power at a fixed price
leaky integrator - impulse response
  • leaky integrator with delta input \[ y[n] = \lambda y[n-1] + (1-\lambda)\delta[n] ]
  • impulse response equation and plot li-04

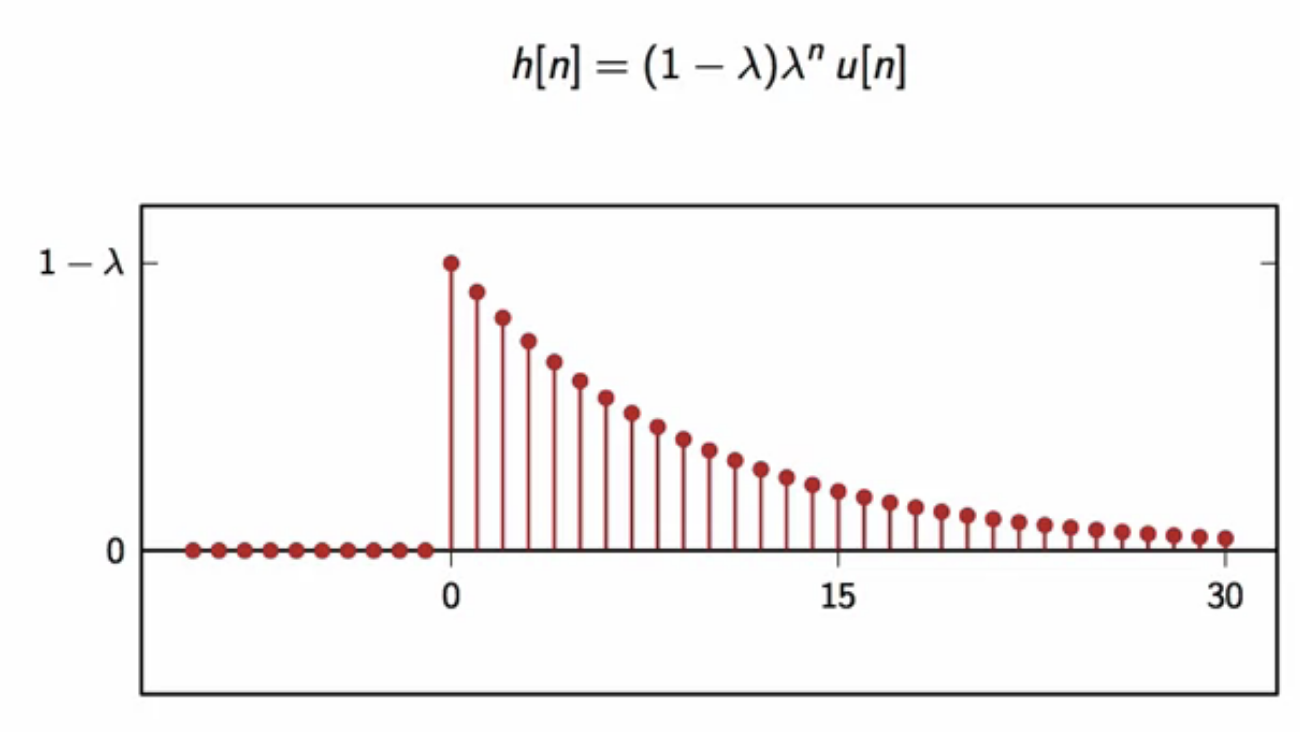
fig: leaky-integrator impulse response

non-leaky integrator comparison
  • discrete-time integrator (non-leaky): \[ y[n] = \sum_{k=-\infty}^{\infty} x[k] ]
    • this is a boundless accumulator
    • which is essentially a discrete-time integral
  • this discrete-time integrator can be rearranged: \[ y[n] = y[n-1] + x[n] ]
  • comparing to the leaky integrator equation: \[ y[n] = \lambda y[n-1] + (1- \lambda) x[n] ]
    • the first term here is the scaled by (\lambda)
    • so only a percent of the past value is kept in the present value
      • the rest is leaked out, or forgotten
    • the leaked out portion ((1-\lambda)) is filled with current input
      • the second term is the current input scaled by ((1-\lambda))
      • the forgotten percent is replaced by an equal percent from the new
    • the sum of there two fraction is fed to the accumulator as the current value
  • so, the leaky integrator filter is similar to a discrete-time integrator, but
    • has leak factor ( \lambda ) that sets accumulated past values percentage to be kept
      • the rest is leaked
    • the leak replace factor (1 - \lambda ) replaces leaked with an equal percent of current input
  • use only ( \lambda < 1) to prevent explosion of accumulation

filter classification

  • filters can be classified according to their impulse-response shape in the time domain
    • Finite Impulse Response Filters (FIR)
    • Infinite Impulse Response Filters (IIR)
    • Causal Filters
    • Non-causal Filters

FIR filters

  • filter’s impulse response has finite-support (with an infinite response)
  • only a finite number of samples are involved in the computation of each output sample
  • moving-average filter is an FIR filter
    • only (M) samples are non-zero and are involved in computation

fc-00

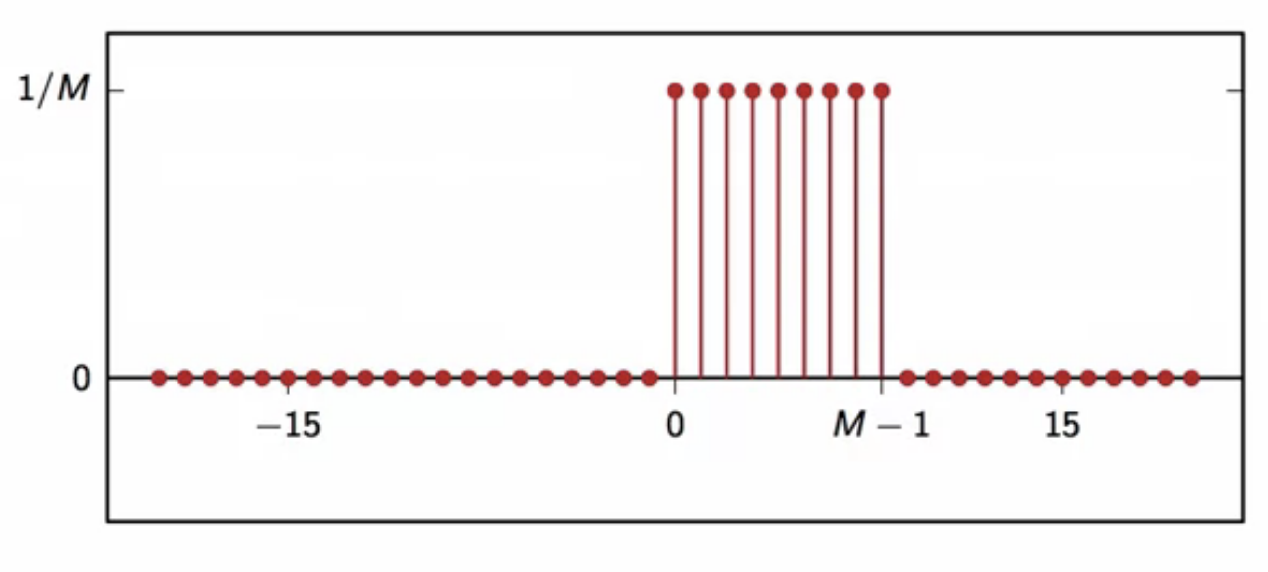
fig: FIR filter example - moving-average filter

IIR filters

  • filter’s impulse response has infinite support
  • a potentially infinite number of samples are involved in the computation of each output sample
    • leaky integrator filter is an IIR filter
    • recursive filters involve infinite samples
  • surprisingly, in many cases the computation can still be performed in a finite-amount of steps
    • a leaky integrator filter output can be computed with only three operations
    • ideal filters are an exception

fc-01

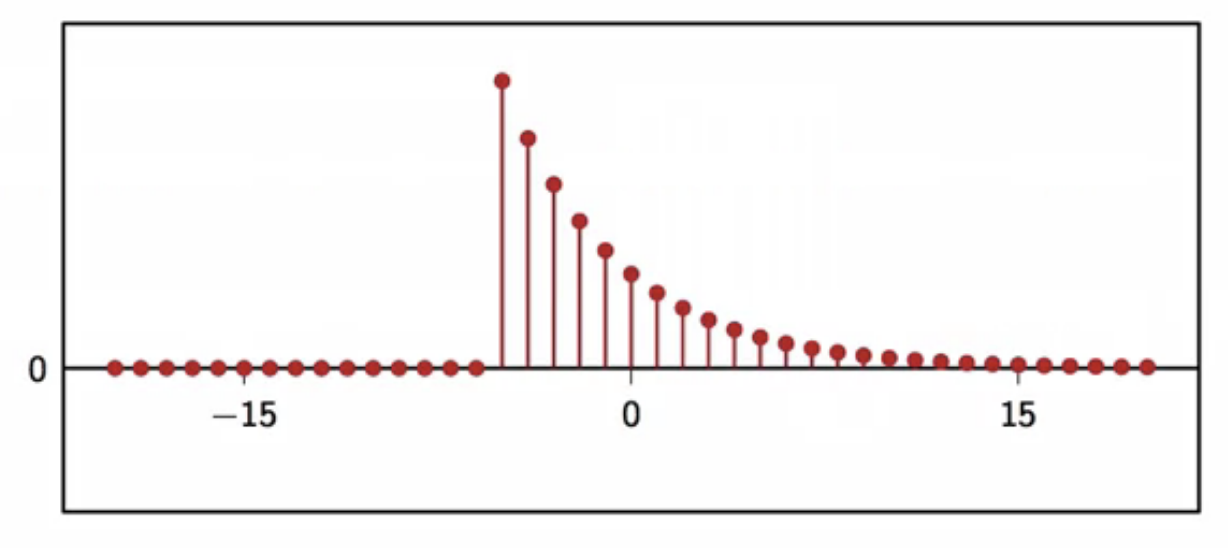
fig: IIR filter example - leaky integrator filter

causal vs. non-causal

  • causal:
    • ony past samples w.r.t present are involved in the output of filter
    • impulse response is zero for (n < 0 )
    • they can run on-line (real-time) since only past values are used
      • physical filters
    • the moving-average filter is a causal filter fig: causal filter example - moving-average filter
  • noncasual:
    • impulse response is non-zero for some (or all) ( n < 0 )
    • is used for static (off-line) dsp, since future values are needed to compute current filter output
      • used in scenarios where the whole data-set is available before dsp is applied
      • batch processing of images is an example

fc-03

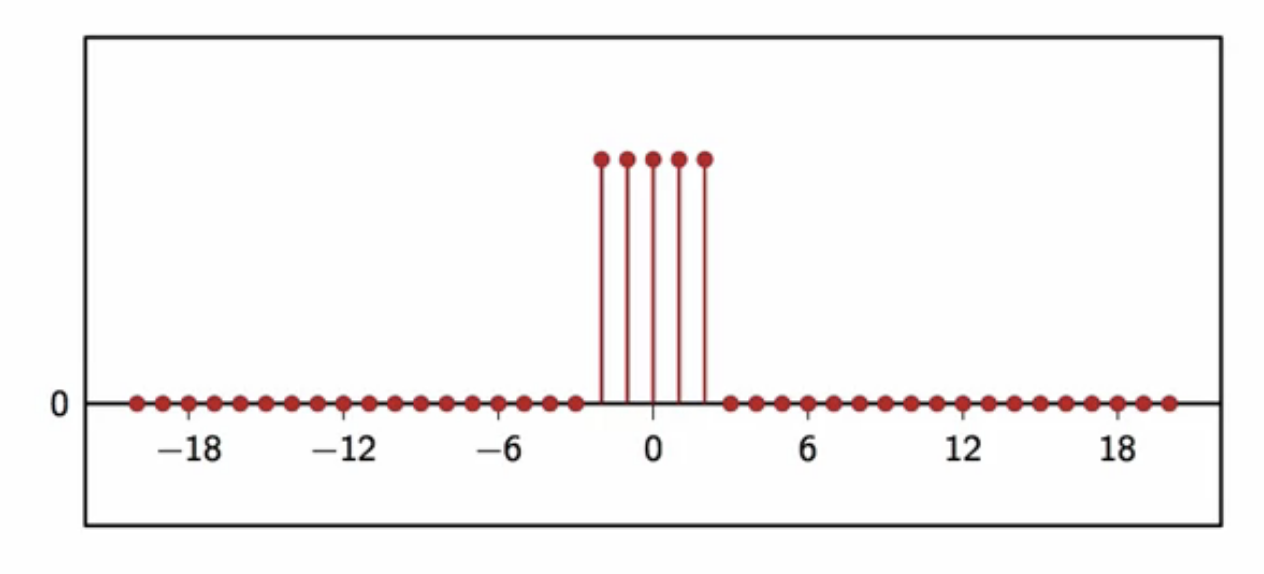
fig: noncausal filter example - zero centered moving-average filter

filter stability

  • main goal:
    • avoid filter “explosions” if the input is nice
  • is a system is stable, it will not behave unexpectedly when its input is well-behaved

BIBO stability

  • in dsp context, a well-behaved signal is a bounded signal
    • ( \vert x[n] \vert < M ) for all (n)
    • a signal whose maximum excursion is known
  • Bounded-Input Bounded-Output system:
    • system output is bounded when its input is bounded

fundamental filter stability theorem

  • a filter is BIBO stable if and only if its impulse response is absolutely summable
    • absolutely summable: sum of magnitudes is not infinity
    • necessary and sufficient condition for stability
  • FIR filters are always stable
  • IIR filter stability has to be checked explicitly with its impulse response
    • leaky-integrator filter stability is guaranteed only for (\vert \lambda \vert < 1 )
  • indirect methods to assess filter stability exist
    • without going through impulse response explicitly

references