[DSP] W05 - Ideal Filters

contents

• frequency classification
• ideal low pass filter
  • formal low pass filter
  • dedicated filter response functions
• derived ideal filters
• demodulation - frequency domain
  • filtering a demodulated signal

---

• based on the frequencies that filters attenuate or boost, they maybe classified into different categories
• low pass filter:
  • lets through only low frequencies
  • kills high frequencies
• high pass filter:
  • reverse operation of low pass filter
• bandpass filter:
  • allow a middle band
  • kills low end and high end
• ideal filers:
  • theoretical best performance filters in each class of filters
  • similar to an ideal engine
  • cannot be implemented in real life
  • a useful paradigm to understand limitations of real-world filters

frequency classification

• based on the shape of magnitude response of filters, they can be categorized into four types
  • lowpass
    • let low frequencies live and kill everything else
  • highpass
    • let high frequencies live and kill the rest
  • bandpass
    • let a band of central frequencies through and kill all else
  • allpass
    • let all frequencies through
    • the magnitude curve is a constant through all frequencies
• this mirrors the time-domain filter classification

• moving-average and leaky-integrator are lowpass filters

• filters can also be classified based on phase change characteristic
  • linear phase
  • non-linear phase

ideal low pass filter

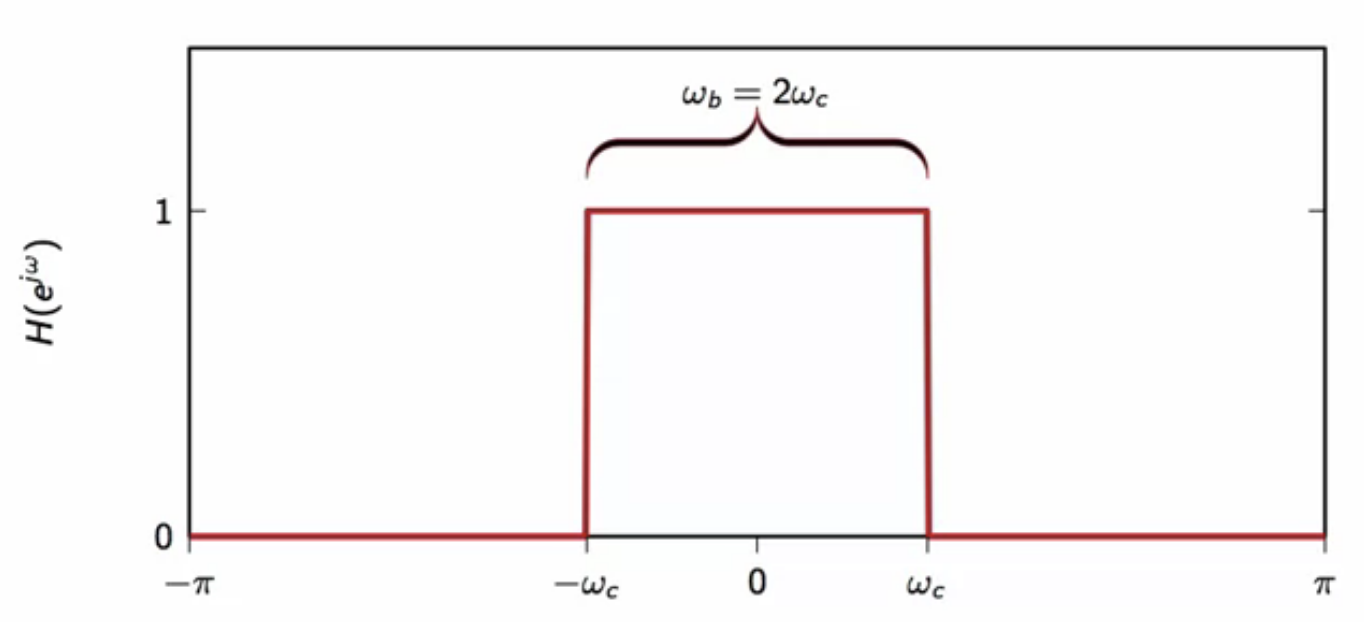
fig: ideal lowpass filter magnitude spectrum

• ${\omega }_c$: cutoff frequency
  • frequencies above ${\omega }_c$ are killed
  • below it are let through filter
  • the magnitude response transistions from $1$ to $0$ at ${\omega }_c$
  • filter bandwidth: ${\omega }_b=2{\omega }_c$

ideally:

• lowpass filters are those which let all low band frequencies through
  • low frequency signals are untouched
  • completely attenuates high frequencies
• magnitude of spectrum is
  • $1$ for the low frequency pass band
  • $0$ for the high frequency stop band
• for this, magnitude response should be a real function
  • zero phase filter
  • no delay is added by the filter

formal low pass filter

$$\begin{array}{ccc}H\left(e^{j\omega }\right)& =\{\begin{array}{cc}1& \text{for}\left|\omega \right|\le {\omega }_c\\ 0& \text{otherwise}\end{array}& \left(2\pi \text{-periodicity implicit}\right)\end{array}$$

• perfectly flat passband
• infinite attenuation in the stopband
• zero-phase (no-delay)

impulse response of ideal lowpass filter

$$\begin{array}{cccccc}h\left[n\right]& =IDFT\left\{H\right(e^{j\omega }\left)\right\}& =\frac{1}{2\pi }{\int }_{-\pi }^{\pi }H\left(e^{j\omega }\right)e^{j\omega n}d\omega & =\frac{1}{2\pi }{\int }_{-{\omega }_c}^{{\omega }_c}{e}^{j\omega n}d\omega & =\frac{1}{\pi n}\frac{e^{j{\omega }_{c}n}-e^{-j{\omega }_{c}n}}{2j}& =\frac{\sin {\omega }_{c}n}{\pi n}\end{array}$$

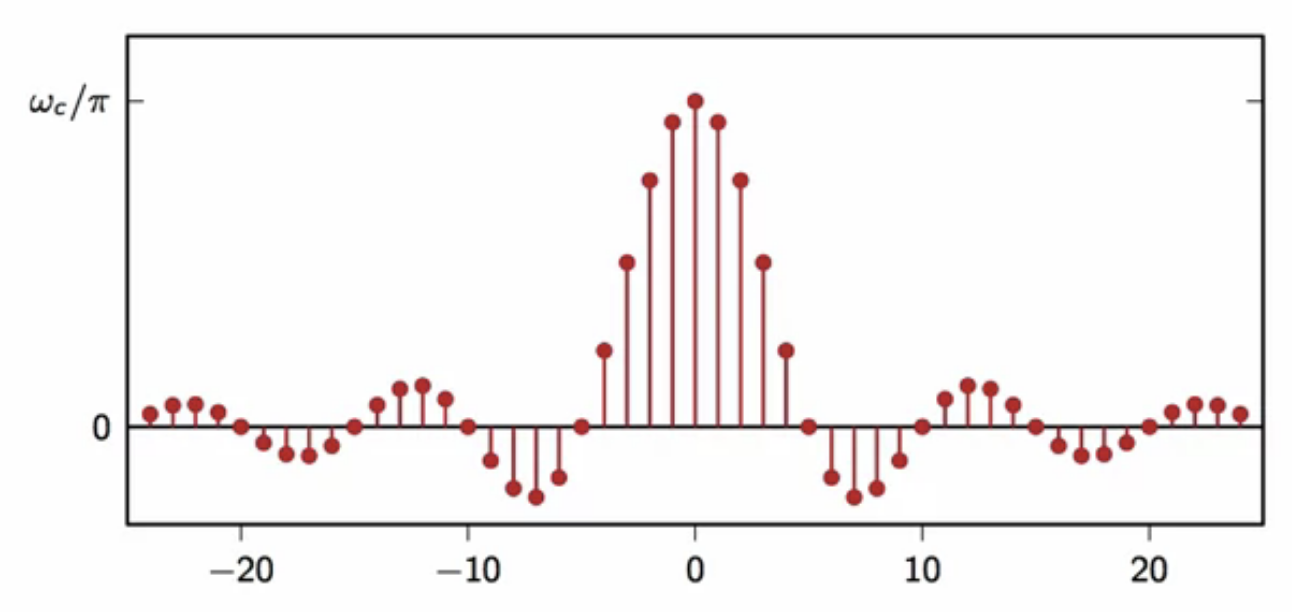
fig: ideal lowpass filter impulse response

• response has a nice oscillatory shape
• response is an infinite support impulse response
  • infinite both to the right and left
• no matter how the convolution is computed, there will always be an infinite number of operations to compute
• this is the ideal behavior and causes issue in real world filter implementation
  • cannot compute the output in a finite amount of time
• this behavior is approximated to build filters that respond in finite time
  • approximation for computable, usable, real-world filters
• the impulse response decays very slowly over time; i.e. @ rate $\frac{1}{n}$
  • a lot of samples are needed for a good approximation

dedicated filter response functions

• the sinc-rect pair: $$\begin{array}{ccccc}rect\left(x\right)& =\{\begin{array}{cc}1& \left|x\right|\le \frac{1}{2}\\ 0& \left|x\right|>\frac{1}{2}\end{array}sinc\left(x\right)& =\{\begin{array}{cc}\frac{\sin \left(\pi x\right)}{\pi x}& x\ne 0\\ 1& x=0\end{array}sinc\left(x\right)& =0\text{when}x\text{is a non-zero integer}\text{sinc}& \text{function here is normalized}\end{array}$$

frequency response of lowpass filter

• frequency response in terms of a $rect$ function of ideal lowpass filter is $$rect\left(\frac{\omega }{2{\omega }_c}\right)$$
  • ${\omega }_c$: cutoff frequency of lowpass filter

impulse response of lowpass filter

• impulse response in terms of a $sinc$ function of ideal lowpass filter is $$\frac{{\omega }_c}{\pi }sinc\left(\frac{{\omega }_c}{\pi }n\right)$$

relationship between lowpass filter impulse and frequency response

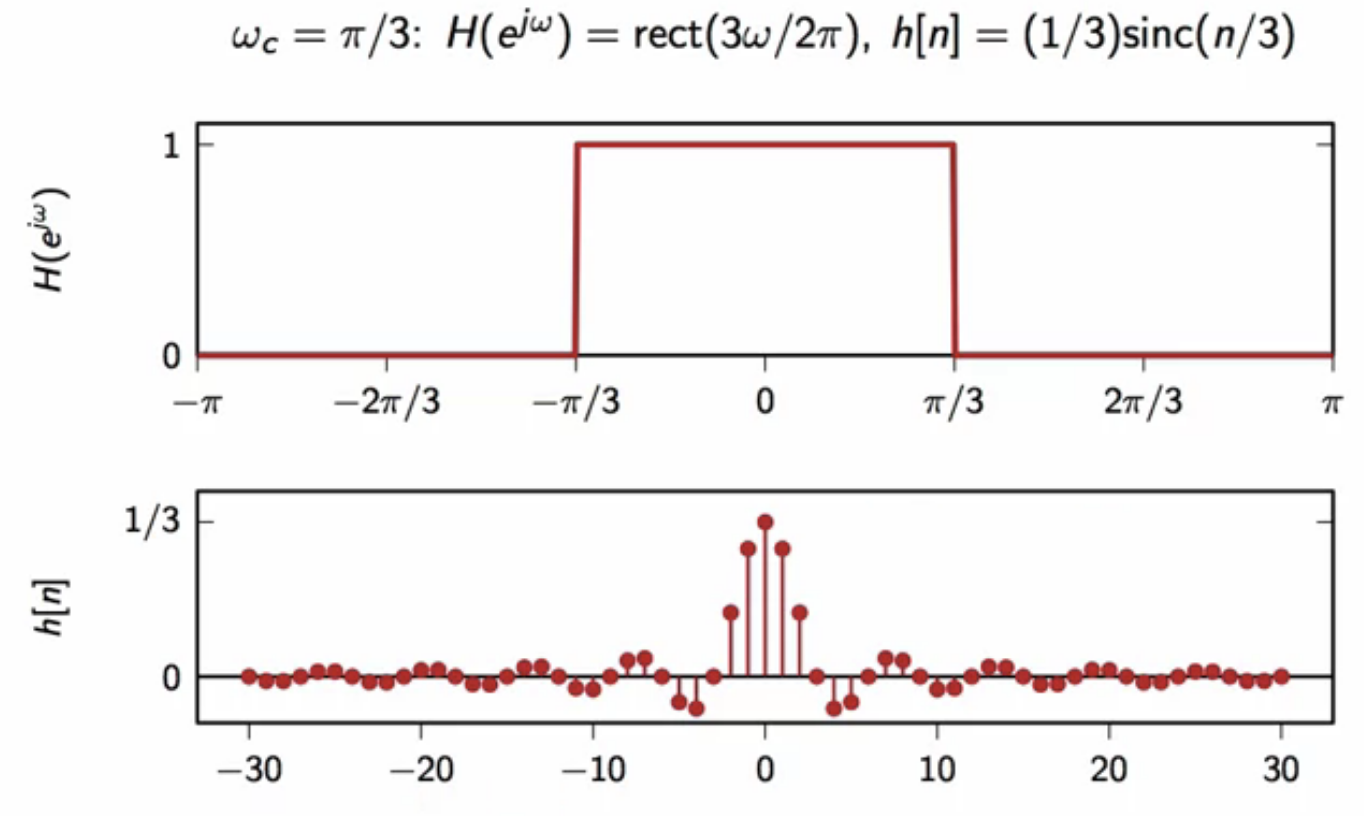
fig: ideal lowpass filter frequency (top) and impulse response (bottom) relationship

• here:
  • ${\omega }_c=\frac{\pi }{3}$

quirks of the ideal lowpass filter

• the $sinc$ function is not absolutely summable
  • consequently, the ideal lowpass is not BIBO stable
• example: $$\begin{array}{ccc}{\omega }_c& =\frac{\pi }{3}h\left[n\right]& =(\frac{1}{3})sinc(\frac{n}{3})\end{array}$$

• consider a bounded input signal for ideal filter $$x\left[n\right]=sign\{sinc(-\frac{n}{3})\}$$

• to compute output of ideal filter, convolve this input and impulse response of ideal lowpass filter $$\begin{array}{cccc}y\left[0\right]& =(x\ast h)\left[0\right]& =\frac{1}{3}\sum _{k=-\infty }^{\infty }|sinc(\frac{k}{3})|& =\infty \end{array}$$
  • the convolution is divergent computation

• however, the divergence is fairly slow

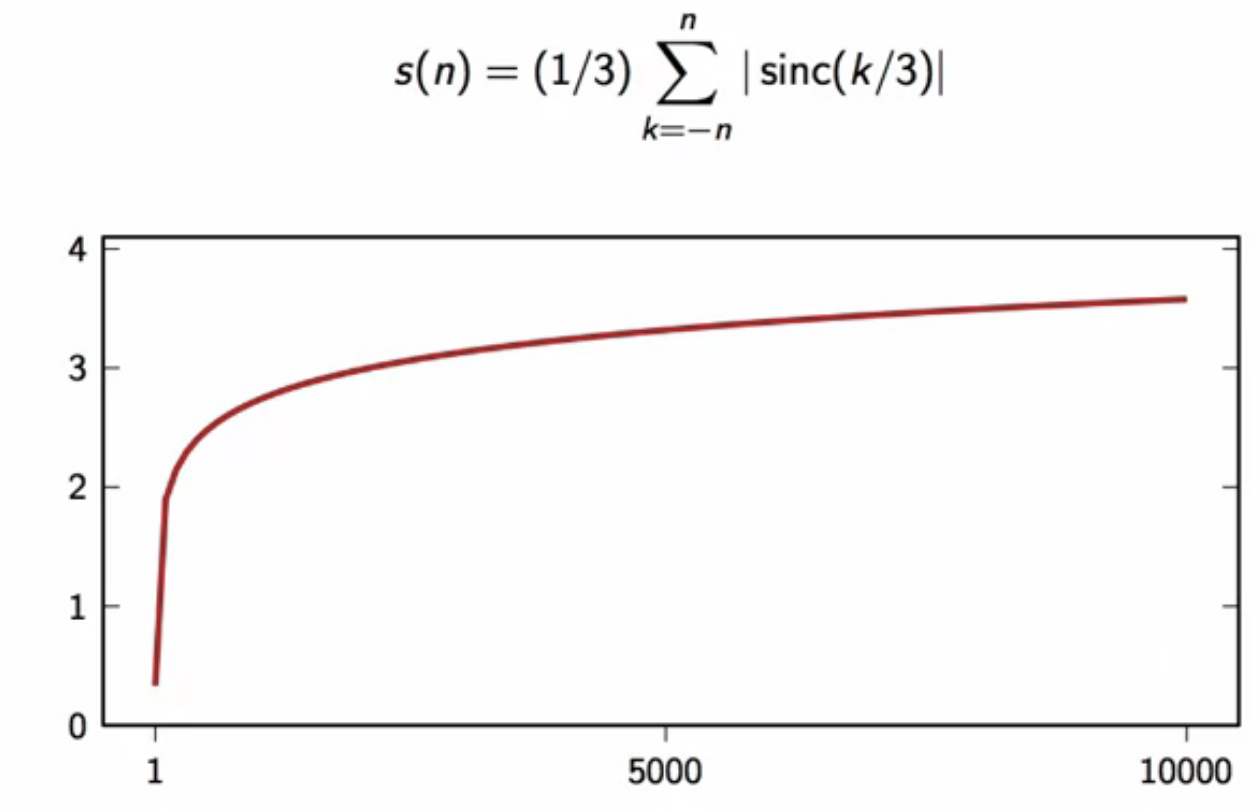
  fig: slow divergence of the ideal lowpass filter convolution with input $x\left[n\right]$

---

derived ideal filters

• a series of other ideal filters can be derived from the ideal lowpass filter

ideal highpass filter

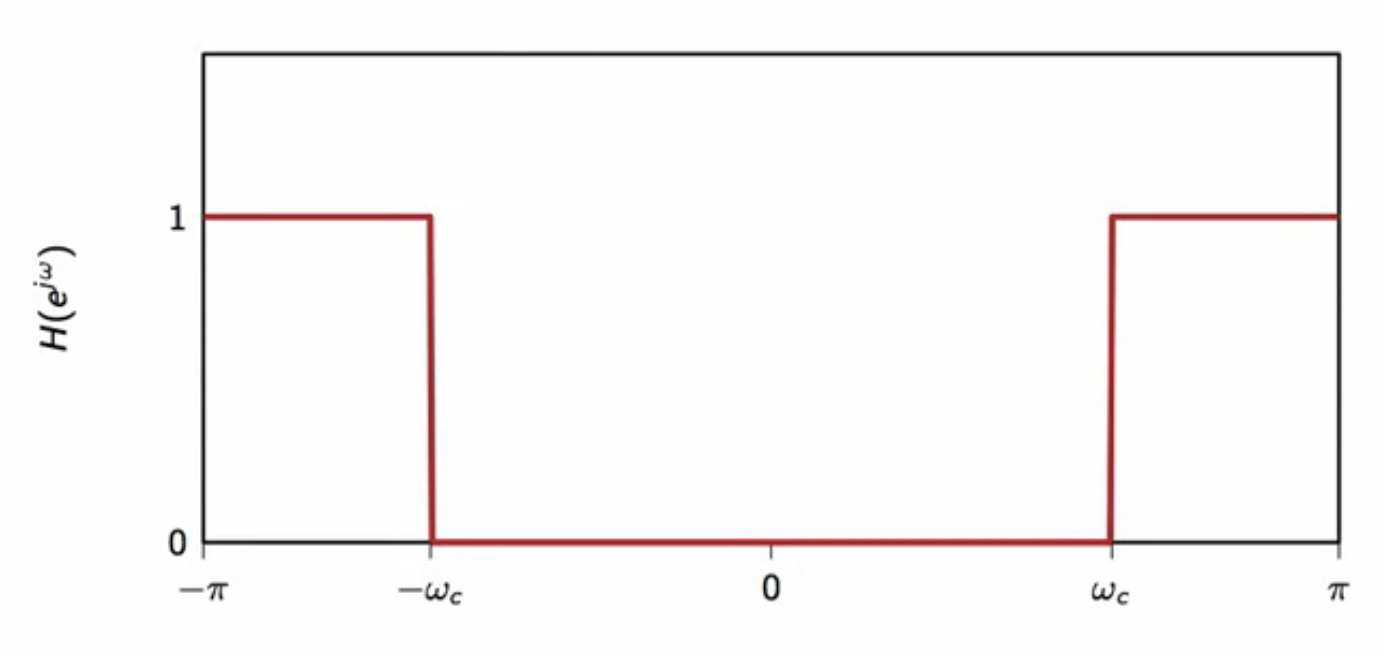
fig: ideal highpass filter magnitude spectrum

formal ideal highpass filter

$$\begin{array}{ccccccc}{H}_{hp}\left(e^{j\omega }\right)& =\{\begin{array}{cc}1& \text{for}\pi \le \left|\omega \right|\le {\omega }_c\\ 0& \text{otherwise}\end{array}& \left(2\pi \text{-periodicity implicit}\right)H_{hp}\left(e^{j\omega }\right)& =1-H_{lp}\left(e^{j\omega }\right)& \text{(highpass-lowpass relationship in frequency)}{h}_{hp}\left[n\right]& =\delta \left[n\right]-\frac{{\omega }_c}{\pi }sinc(\frac{{\omega }_c}{\pi })& \text{(highpass-lowpass relationship in time)}\end{array}$$

• it can be seen that the ideal highpass is a complementary filter of an ideal lowpass filter in the frequency domain

ideal bandpass filter

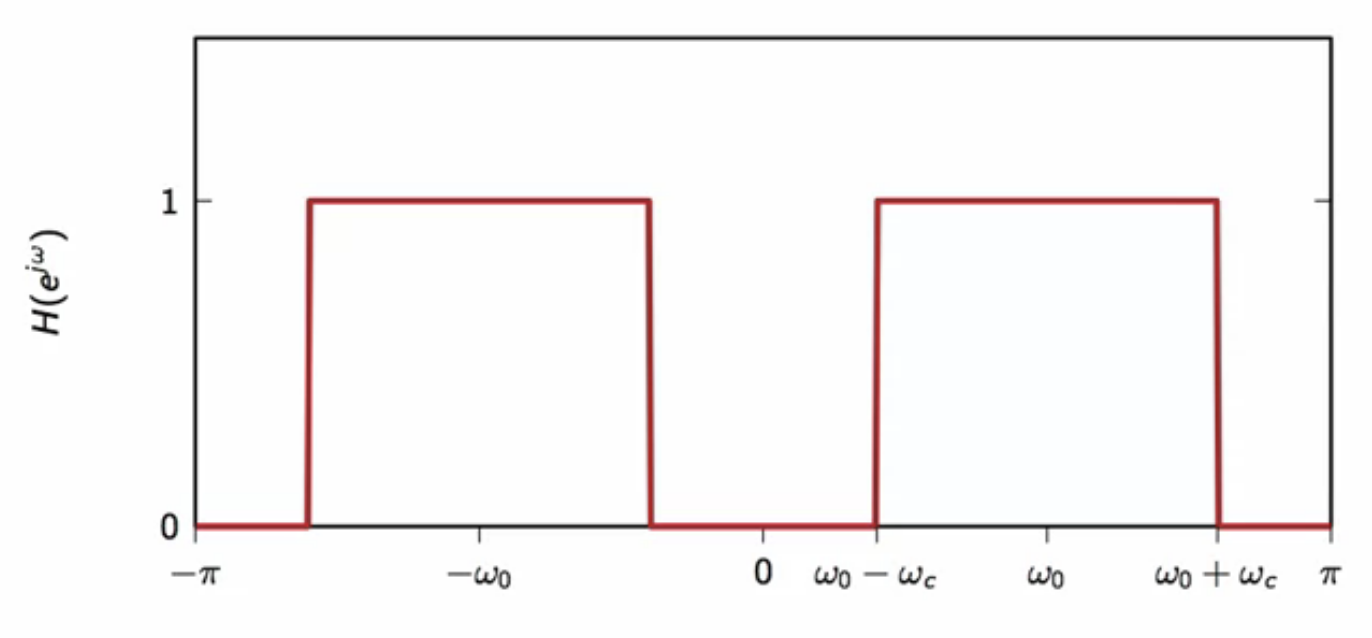
fig: ideal bandpass filter magnitude spectrum

• this is derived from the ideal lowpass filter by modulating them with a cosine wave

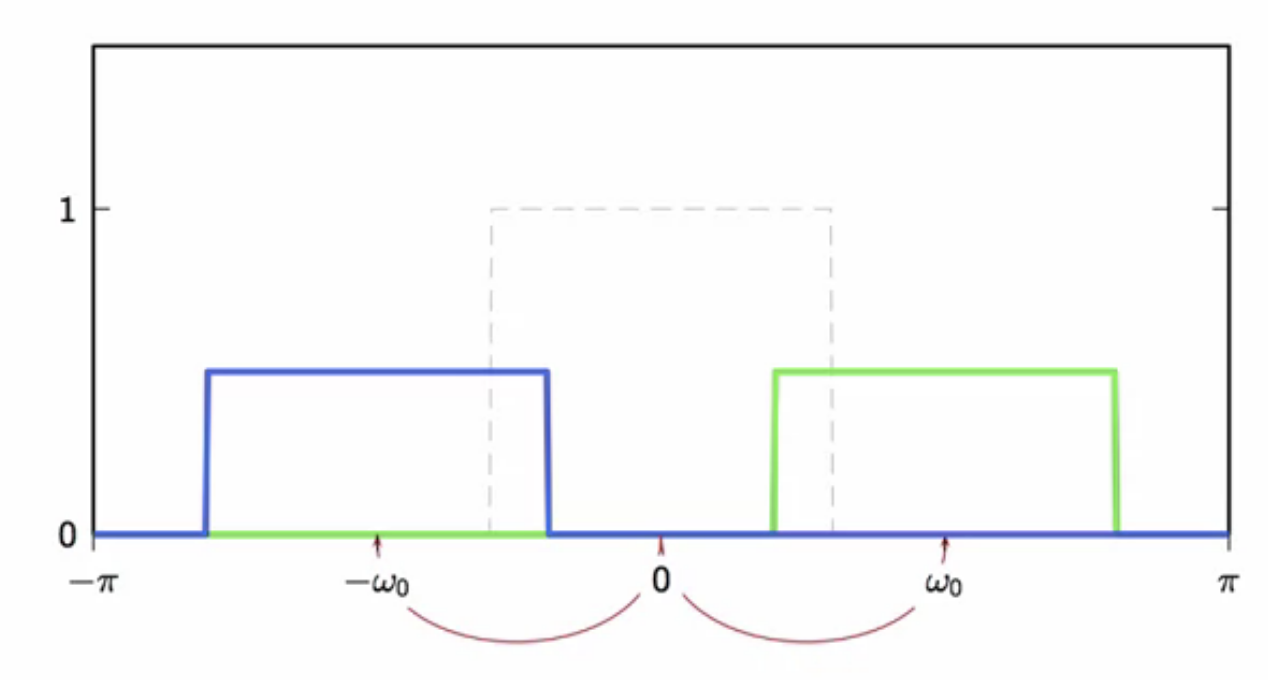
fig: ideal lowpass filter modulated with cosine wave to obtain ideal bandpass

formal ideal bandpass filter

$$\begin{array}{ccccc}{H}_{bp}\left(e^{j\omega }\right)& =\{\begin{array}{cc}1& \text{for}|\omega \pm {\omega }_0|\le {\omega }_c\\ 0& \text{otherwise}\end{array}& \left(2\pi \text{-periodicity implicit}\right)h_{bp}\left[n\right]& =2\cos \left({\omega }_{0}n\right)\frac{{\omega }_c}{\pi }sinc(\frac{{\omega }_c}{\pi }n)& \text{(highpass-lowpass relationship in time)}\end{array}$$

---

demodulation - frequency domain

• time domain demodulation concepts
  • apply sinusoidal modulation to $x\left[n\right]$ $$y\left[n\right]=x\left[n\right]\cos {\omega }_{0}n$$
  • demodulate by multiplication with carrier $$x\prime \left[n\right]=y\left[n\right]\cos {\omega }_{0}n$$
  • demodulated signal contains unwanted high frequency components
  • these unwanted high frequency components are filtered out with a lowpass filter

filtering a demodulated signal

• consider a signal in the frequency domain $X\left(e^{j\omega }\right)$

  

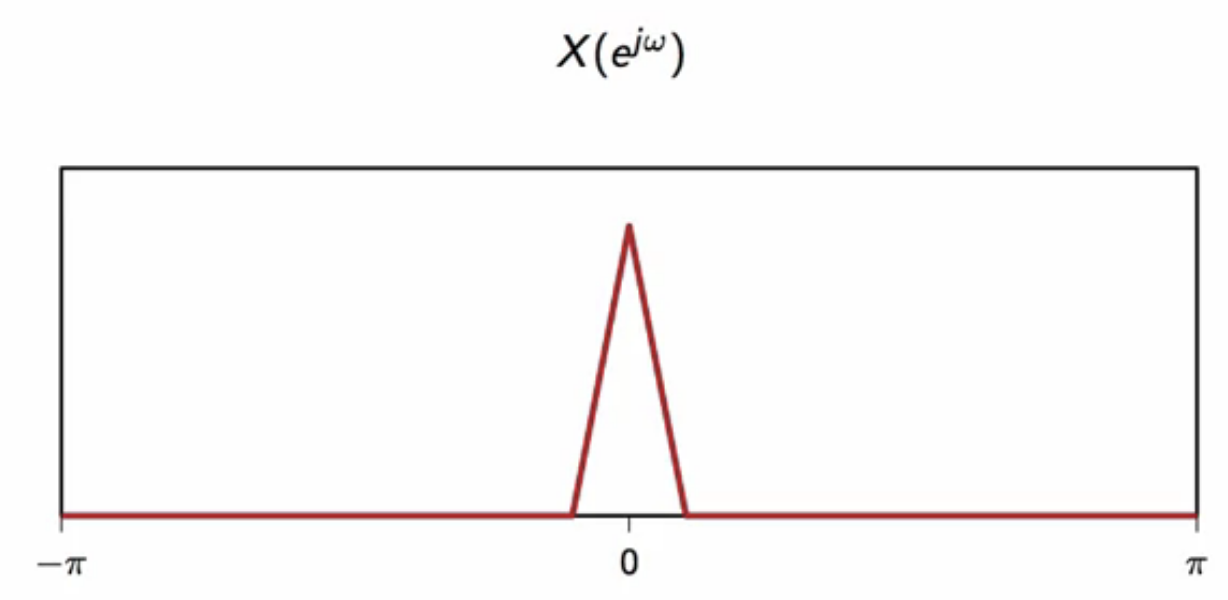
  fig: signal in frequency domain $X\left(e^{j\omega }\right)$

• this is then modulated to get two half amplitudes at the modulation frequency

  

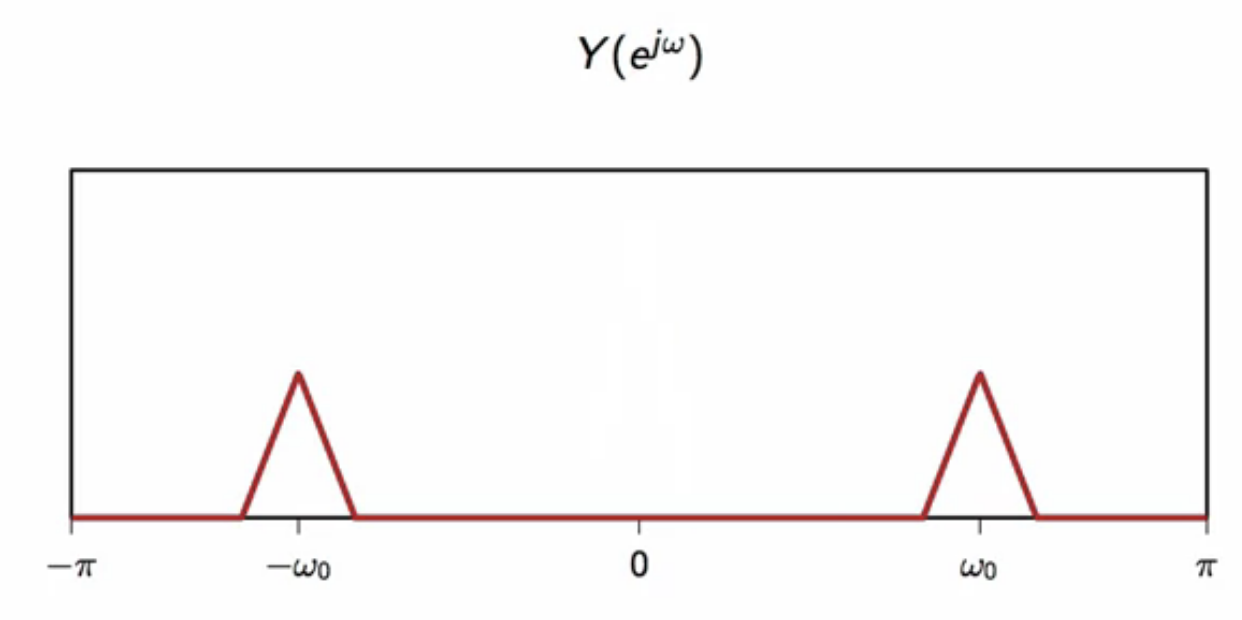
  fig: modulate $X\left(e^{j\omega }\right)$ signal in frequency domain

• this has a periodicity of $2\pi$ in the frequency domain

  

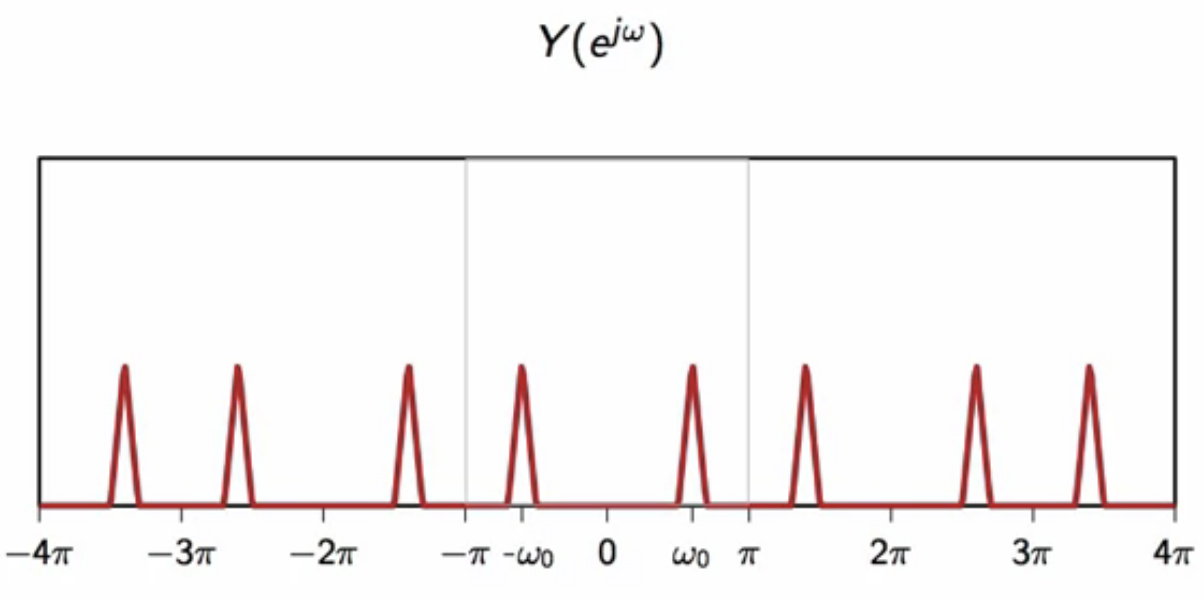
  fig: extended bounds to reveal periodicity of modulated signal $X\left(e^{j\omega }\right)$

• this is then multiplied by $\cos {\omega }_0$ to demodulate, which yields two components

  

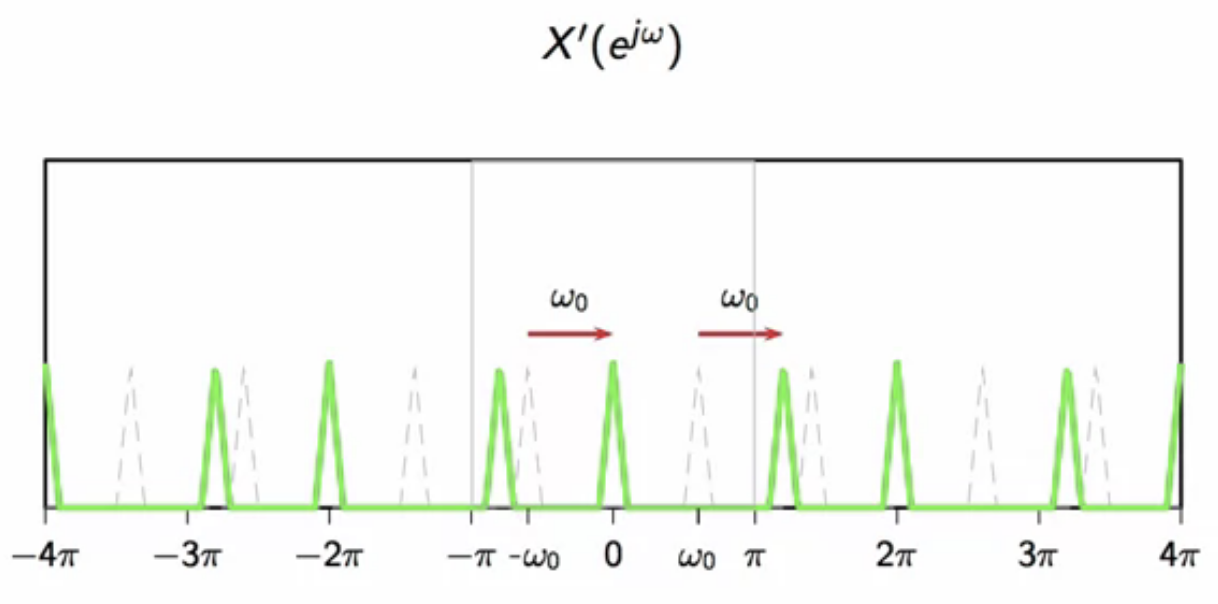
  fig: one copy of the demodulated signal

  

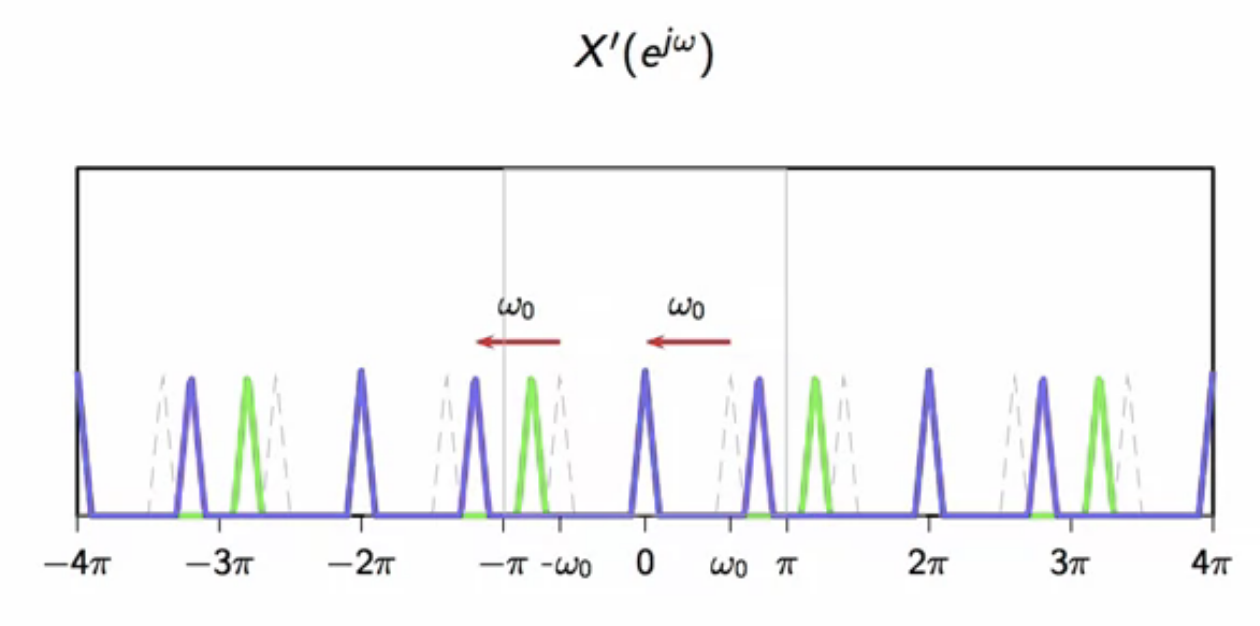
  fig: second copy of the demodulated signal

• to get the full demodulated signal, the two components are summed together to get

  

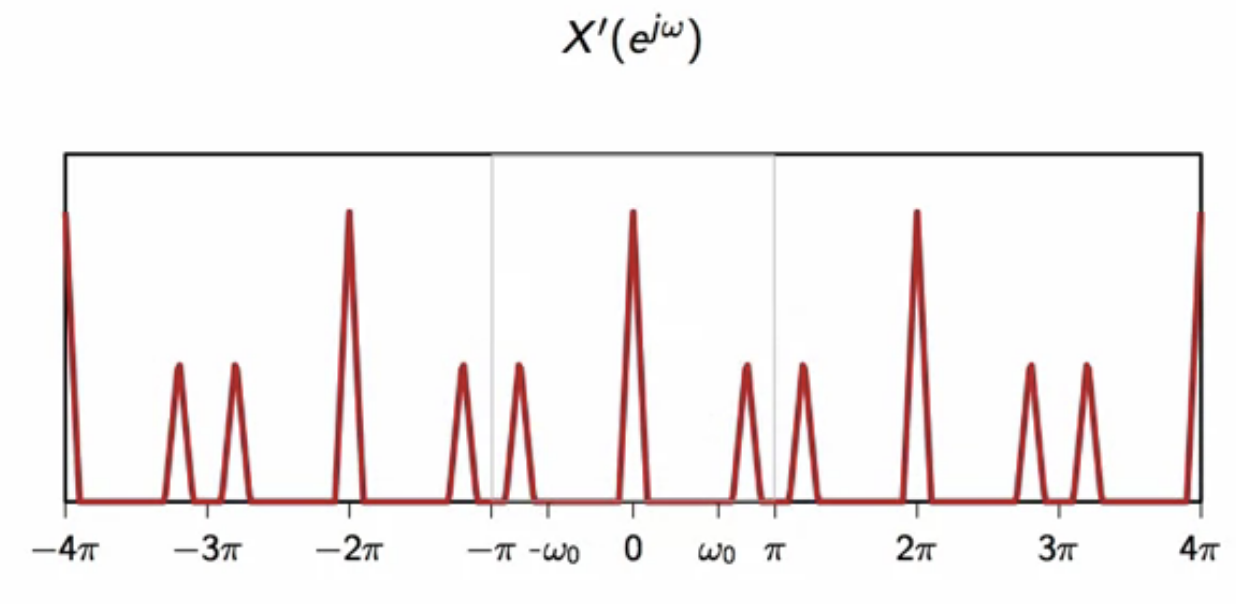
  fig: sum of the components of the demodulated signal

• examining a single period of this summation in $[-\pi ,\pi ]$

  

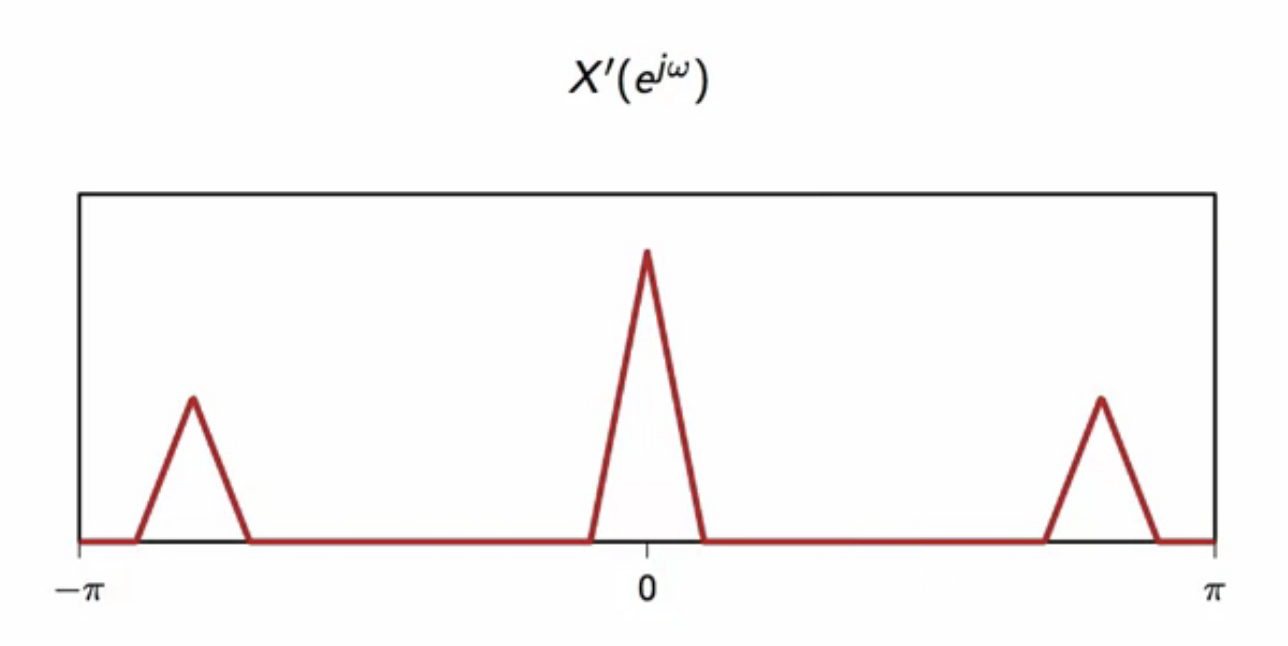
  fig: single period (between $[-\pi ,\pi ]$) of the summed signal

• here, spurious high frequency components near $\pi$ has to be filtered out

• this is achieved using a lowpass filter

  

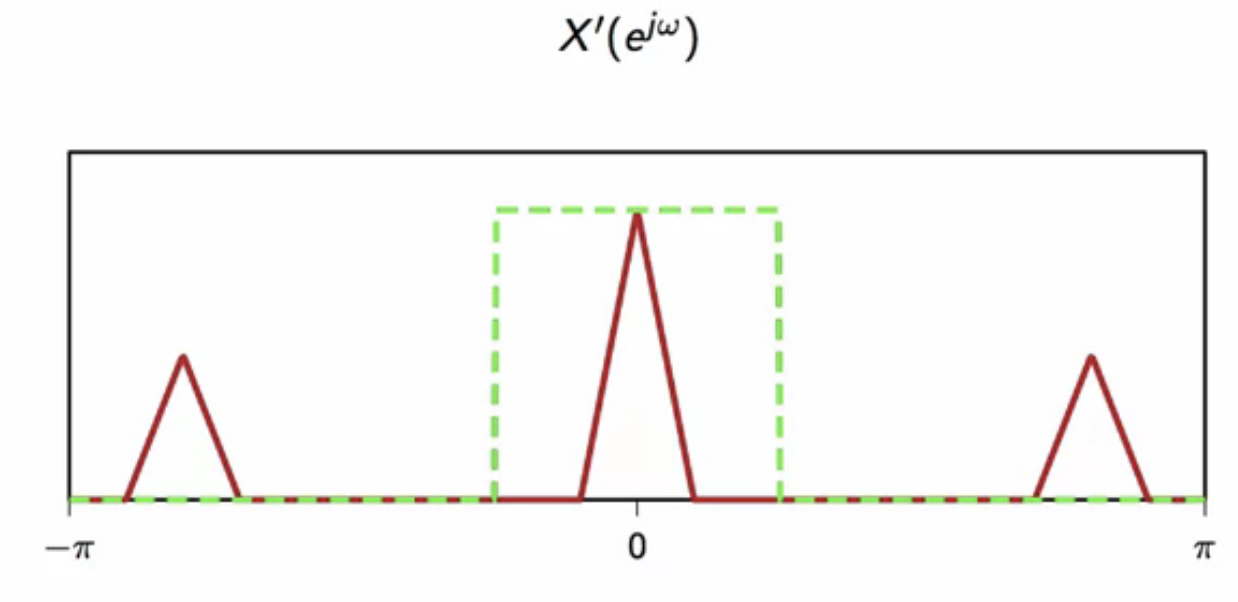
  fig: low pass filter applied to demodulated signal

• the original signal is obtained as the output of the filter

  

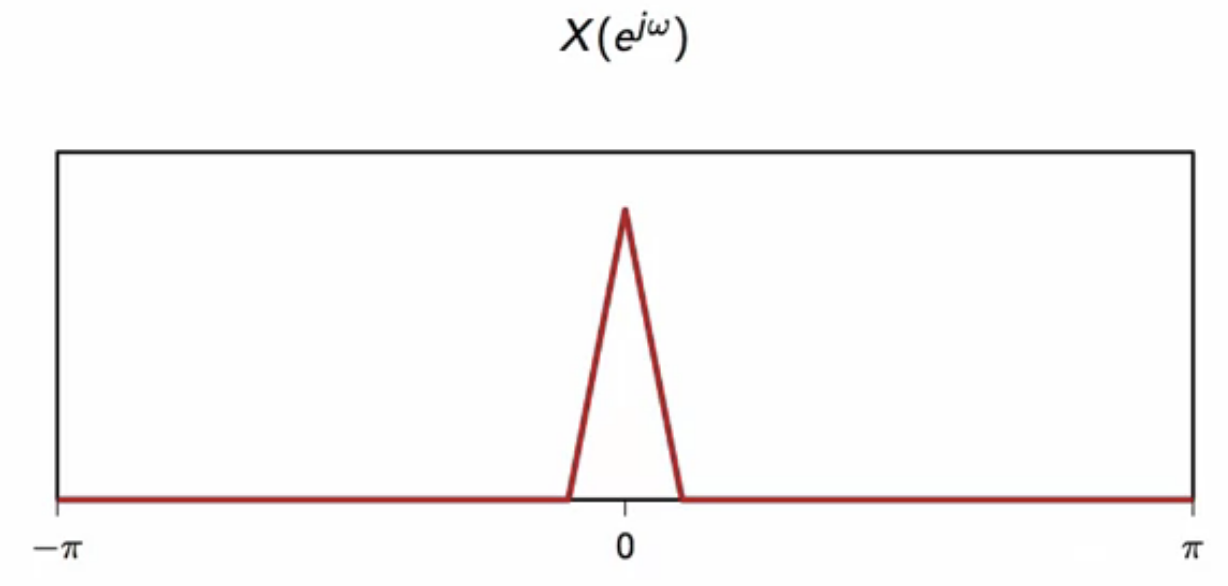
  fig: original signal obtained from filtering demodulated signal

---

references

• ecole dsp - filters