contents

  • ideal filters cannot be implemented in practice
    • its impulse response is a two sided infinite support sequence
  • strategies to approximate ideal filter behavior with practical structures are explored

imitation strategy

  • replicate the structure of either the impulse response or the frequency response of ideal filters
  • three fundamental methods to approximate ideal filters:
    • impulse truncation
    • the window method
    • frequency sampling
  • this strategy is rather limited

impulse truncation

  • this is approximation by truncation of the impulse response of the impulse response
  • procedure:
    • pick (\omega_c)
    • compute ideal impulse response (h[n] )
    • truncate (h[n]) to a finite-support ( \hat{h}[n] )
    • ( \tilde{h}[n] ) defines an FIR filter
  • FIR approximation of length ((M = 2N + 1 ) \[ \hat{h}[n] = \Bigg { \begin{matrix} \frac{\omega_c}{\pi} sinc \big( \frac{\omega_c}{\pi} n \big ) & \vert n \vert \leq N \ 0 & \text{otherwise} \end{matrix} ]

pros

  • MSE is minimized by symmetric impulse truncation filter around zero
  • MSE computation between ideal and truncated filter [ \begin{align} MSE & = \frac{1}{2\pi} \int_{-\pi}^{\pi} \vert H(e^{j\omega}) - \hat{H}(e^{j\omega}) \vert^2 d\omega _
    & = \vert\vert H(e^{j\omega}) - \hat{H}(e^{j\omega}) \vert\vert^2 _
    _& = \vert\vert h[n] - \hat{h}[n] \vert\vert^2 _
    _& = \sum    {-\infty}^{\infty} \vert h[n] - \hat{h}[n] \vert^2 \end{align} ]

cons

  • gibbs phenomenons occurs during approximation
    • approximation always has some error to approximation near transition frequency
  • the maximum error around the cutoff frequency is around 9% of the height of the jump
    • regardless of (N)
    • this is the gibbs error

fd-00

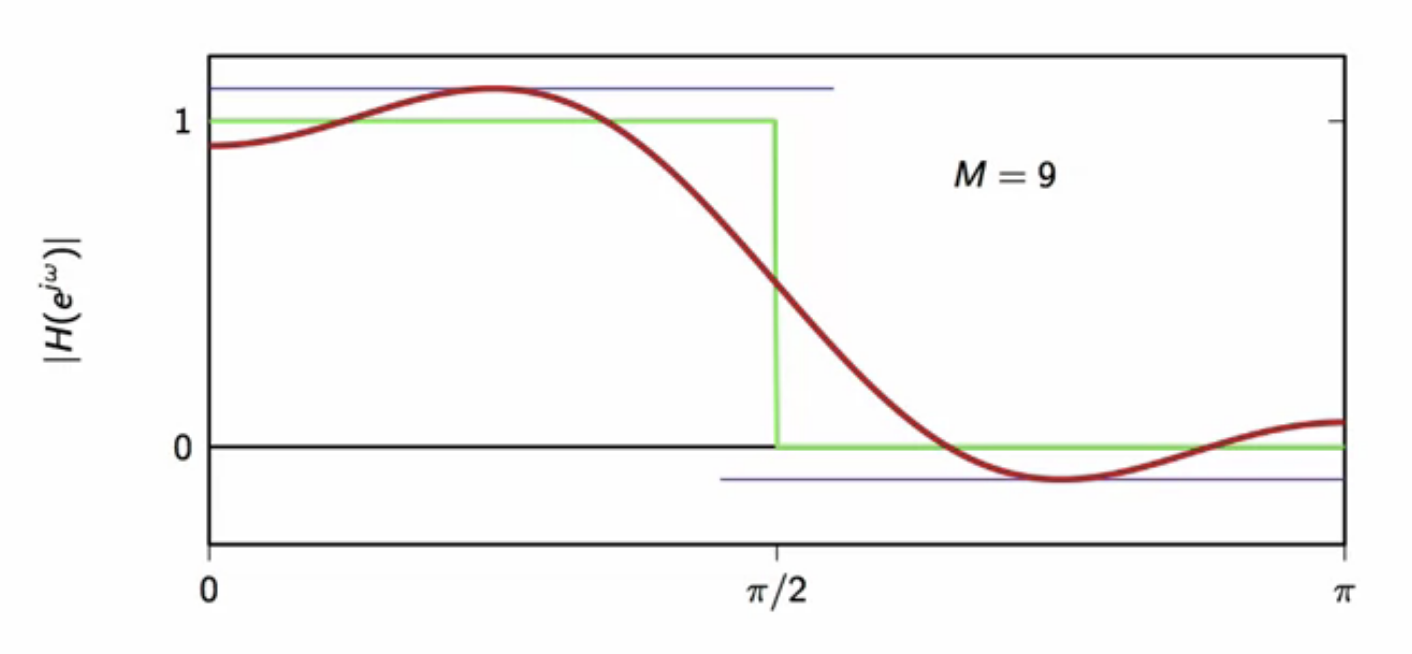
fig: ideal vs truncated - truncated (M=9)

fd-01

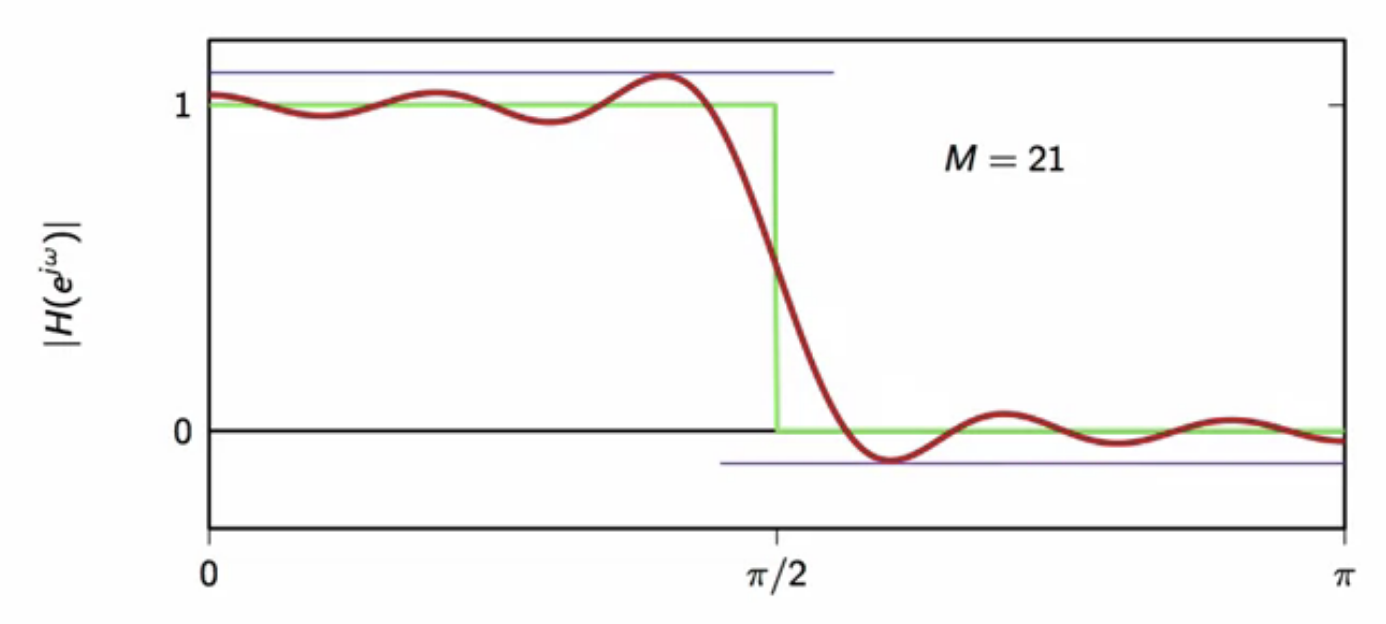
fig: ideal vs truncated - truncated (M=21)

fd-02

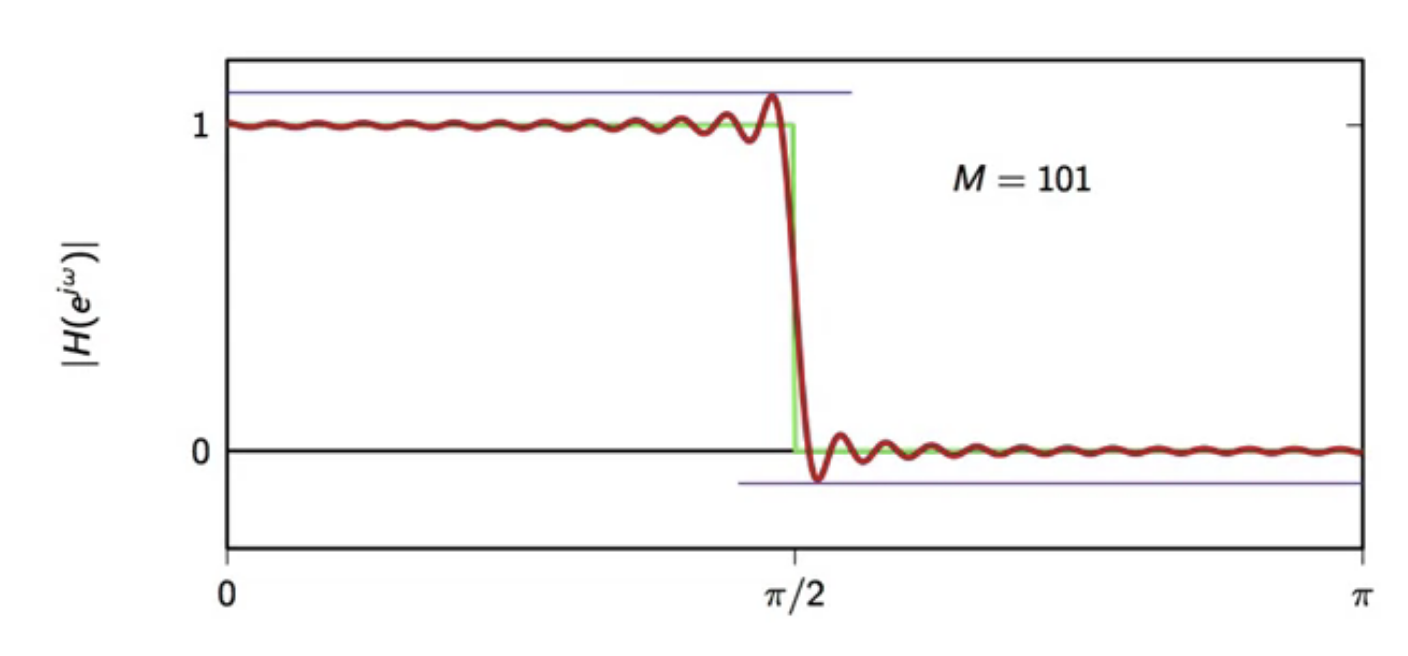
fig: ideal vs truncated - truncated (M=101)

fd-03

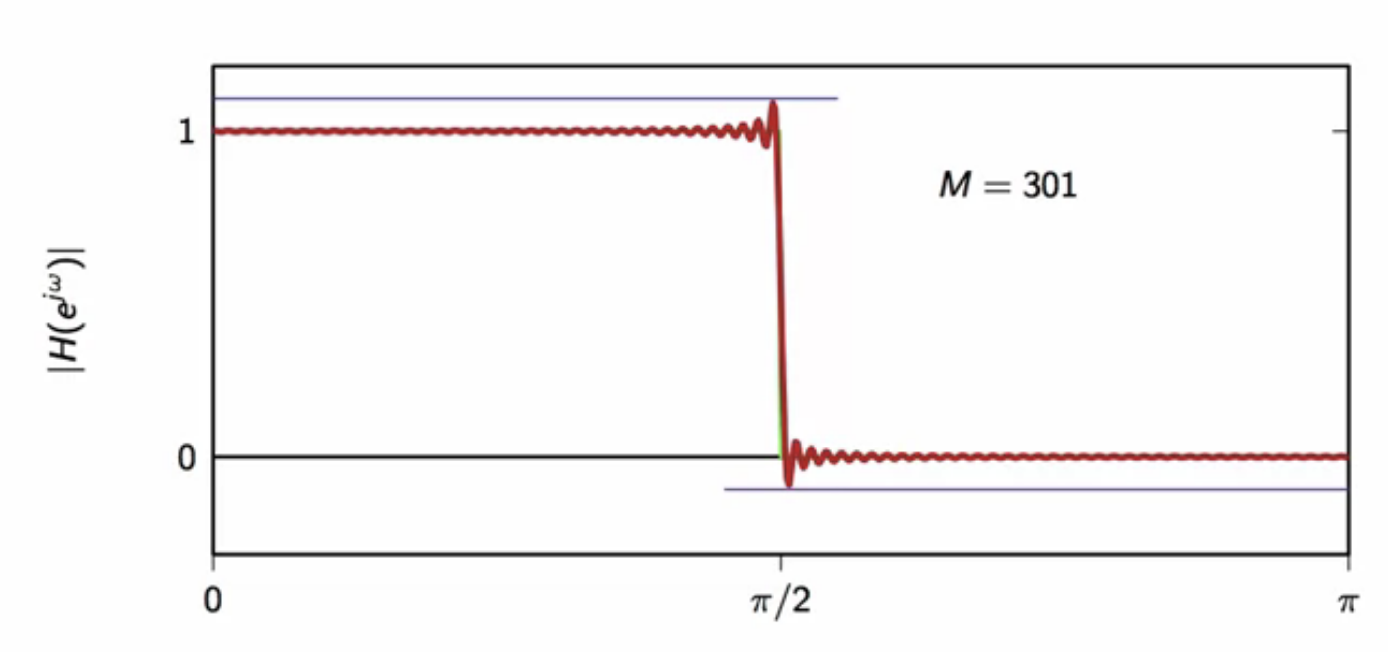
fig: ideal vs truncated - truncated (M=301)

  • Gibbs phenomenon always occurs when a discontinuous function is approximated

modulation theorem

  • convolution theorem states that the fourier transform of the convolution of two sequences is
    • the product of the sequence fourier transforms in the frequency domain \[ DTFT { (x * y)[n] } = X(e^{j\omega})Y(e^{j\omega}) ]
  • modulation theorem gives the result for the fourier transform of the product of two sequences
    • says fourier transform of product of two sequences is the convolution of their fourier transforms in the frequency domain \[ DTFT { x[n]y[n] } = (X*Y)(e^{j\omega}) ]

convolution of DTFTs

  • in the space of infinite support sequences ( \mathbb{C}^\infty )
    • convolution is defined in terms of the inner product between sequences
  • convolution between ( x ) and ( y ) is the inner product between
    • ( x ) conjugated and
    • ( y ) time reversed and delayed by ( n )

[ \begin{align} (x y)[n] & = \langle x^ [k], y[n-k] \rangle
& = \sum_{n = -\infty}^{\infty} x[k]y[n-k] \ \end{align} ]

  • similarly, in the space of DTFTs (L_2([-\pi,\pi]) ):
    • the convolution of DTFTs is defined as [ \begin{align} (X Y)(e^{j\omega}) & = \langle X^ (e^{j\sigma}), Y^* (e^{j(\omega - \sigma)}) \rangle d\sigma
      & = \frac{1}{2\pi} \int_{-\pi}^{\pi} X (e^{j\sigma})Y(e^{j(\omega - \sigma)}) d\sigma
      \end{align} ]
  • modulation theorem proof can be found in DSP textbooks and in the reference

\[ IDFT { (X * Y)(e^{j\omega}) } = x[n]y[n] ]

window function

  • window function method is a generalization of the impulse truncation method where a different window shape may be used
  • truncation can be expressed as follows \[ \hat{h}[n] = h[n]w[n]
    \text{where } w[n] \text{ is the truncation (window) function}
    w[n] = \Bigg { \begin{matrix} 1 & \vert n \vert \leq N \ 0 & \text{otherwise } \end{matrix} ]

fd-04

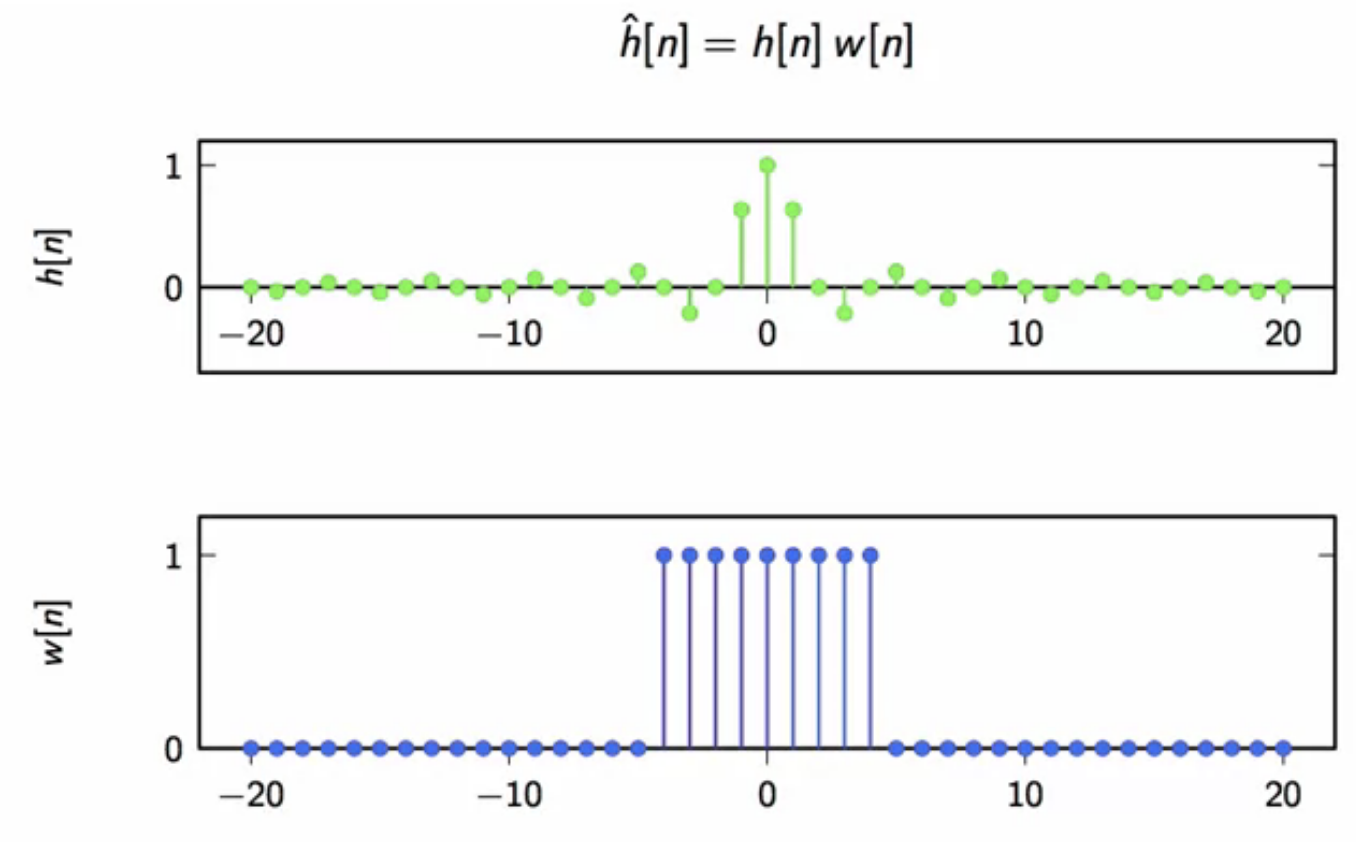
fig: the ideal filter impulse response (top) and the truncation multiplier signal (bottom)

  • given this, the goal is to find the fourier transform of the truncated filter \[ \hat{H}(e^{j \omega}) = ? ]

fd-05

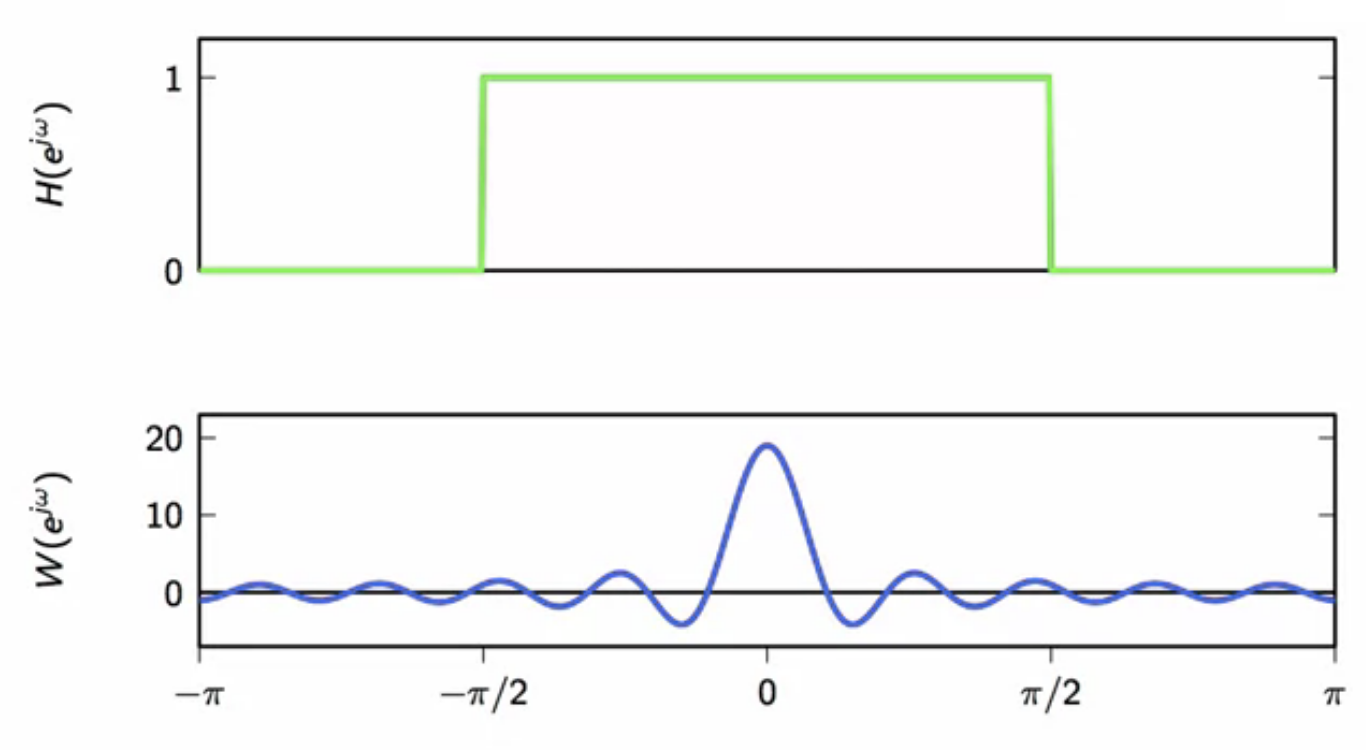
fig: fourier transforms of the ideal filter impulse response (top) and the truncation multiplier signal (bottom)

[ \begin{align} \hat{H}(e^{j\omega}) & = (H * W)(e^{j\omega})
H(e^{j\omega}) & \rightarrow \text{the rect function}
W(e^{j\omega}) & = \frac{ \sin \big ( \frac{ \omega (2N + 1) }{2} \big ) }{ \sin \big ( \frac{\omega}{2} \big ) }
\end{align} ]

frequency domain

  • graphically, the progression of the convolution of the implicit frequency domain convolution of
    • ideal filter impulse response (top)
    • truncation multiplier signal (bottom) fig: low (\omega)

      fig: (\omega) at transition

      fig: (\omega) in ideal lowpass filter passband

      fig: (\omega) deeper in ideal lowpass filter passband

      fig: (\omega) at center of ideal lowpass filter passband

      fig: (\omega) moving away from center of ideal lowpass filter passband

      fig: (\omega) reaching exit of ideal lowpass filter passband

      fig: (\omega) at other transition

      fig: (\omega) in ideal lowpass filter stopband

  • as observed above, the shape of the fourier transform of the approximate filter depends on the fourier transform of the truncation multiplier function ( w[n] )
  • the mainlobe is the red lobe in the below fig
    • the width of this mainlobe determines how quickly the approximated filter will transform from stopband to passband
  • the area in red in below fig are the sidelobes
    • the amplitude of the sidelobes determines the amount of error on either sides of the passband at the transition
      • i.e. the gibbs error fig: fourier transform of the truncation multiplier function ( w[n] )
  • desired qualities in the fourier transform of the truncation multiplier function ( w[n] ):
    • narrow mainlobe so transition is quick
    • small sidelobes for minimal gibbs error
    • short window so FIR is efficient
    • these requirements are conflicting
  • triangular window is an alternative to the rectangular window
    • this reduces the gibbs error
    • tradeoff is a wider main lobe
      • so slow transformation between passband and stopband

fd-16

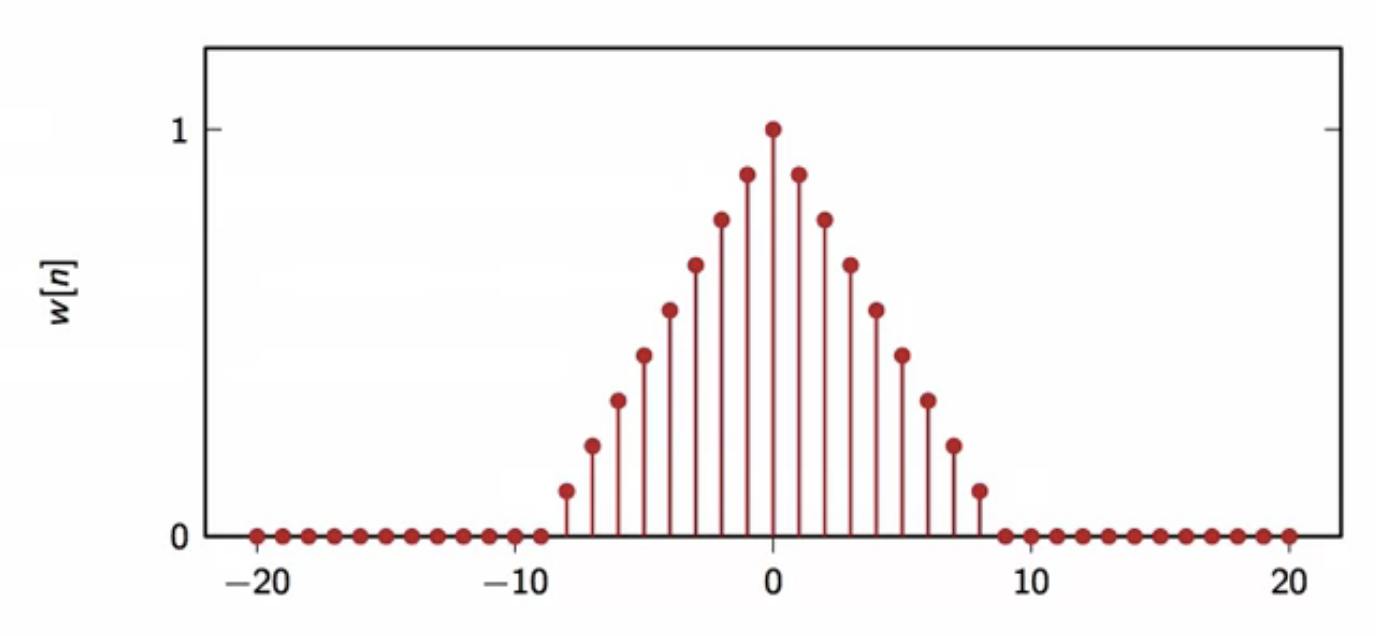
fig: triangular window

frequency sampling

  • a different method of approximating an ideal filter
  • procedure
    • draw desired frequency response ( H(e^{j\omega}) ) in frequency domain
    • sample (M) values @ regular intervals of ( \omega_k = \Big( \frac{2\pi}{M}k \Big) ) between ([-\pi,\pi])
    • compute IDFT of samples values
    • use result as an (M)-tap impulse response ( \hat{h}[n] )
      • this impulse response is the approximated filter characteristic
  • example: fig: desired response expressed (drawn) in frequency domain

    fig: 11 samples taken from desired response

    fig: rearrange sampled values according to DFT notation

    fig: compute IDFT - impulse response of approximated filter

pros

  • quick and dirty method to get an approximated filter

cons

  • not optimal
  • DFT of the obtained finite-support filter has to converted to the DTFT representation
    • DTFT is optimal only for infinite-length signals
    • DFT is optimal for finite-support signals
  • in the process of converting DFT to DTFT, there is interpolation of multiple signals involved
    • frequency response is the interpolation of frequency samples
  • interpolator is transform of N-tap rectangular window (again)
    • so no control over mainlobe and sidelobes
    • gibbs error reigns supreme

fd-21

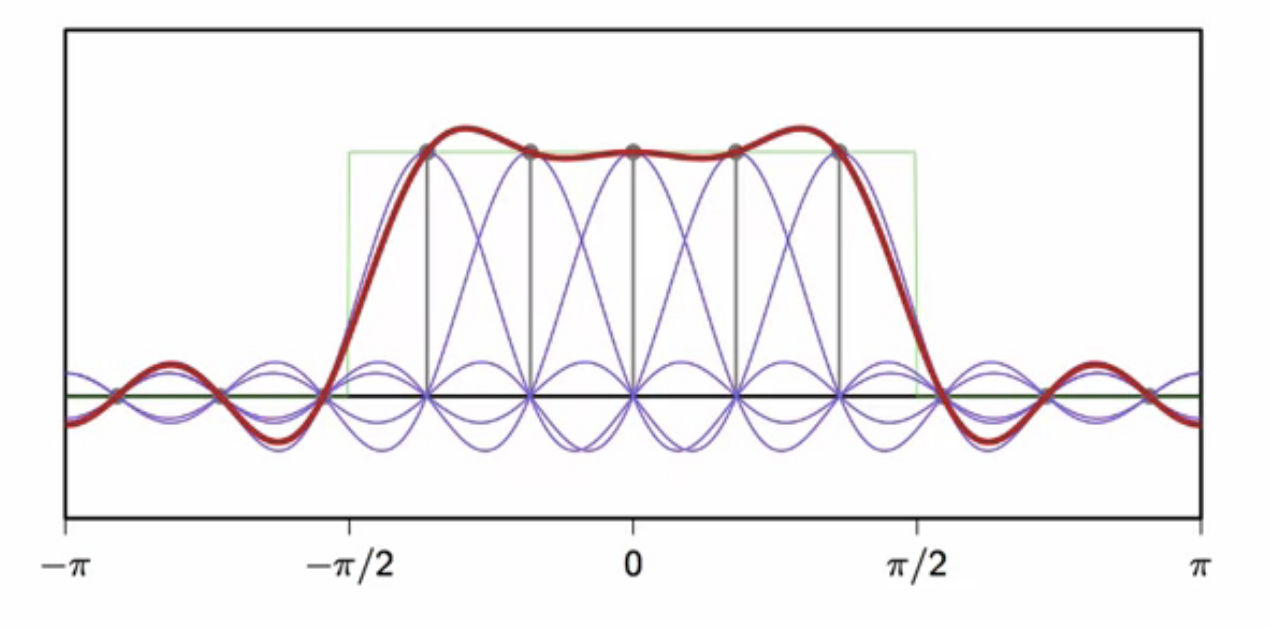
fig: green - desired frequency response; blue - frequency sample interpolation; red - DTFT of obtained filter

references