contents

simple filters

  • simple filters solve a lot of dsp problems
    • mastering simple filters is important
  • low order transfer functions can be easily understand just by looking at their zero-pole plot
    • their design and tuning is intuitive
  • simple filters can be derived from ideal filters by tuning the zero-pole plot
    • complex poles and zeros in complex conjugate pairs are added to the zero-pole plot to obtain real filters
    • zero and poles position is set as required to enable desired filter function
  • simple filter examples
    • moving average
    • leaky integrator

leaky-integrator

  • let only low frequencies pass
  • finds application in
    • removing high frequency components, which usually is noise
    • useful in audio, communication and control systems

filter structure

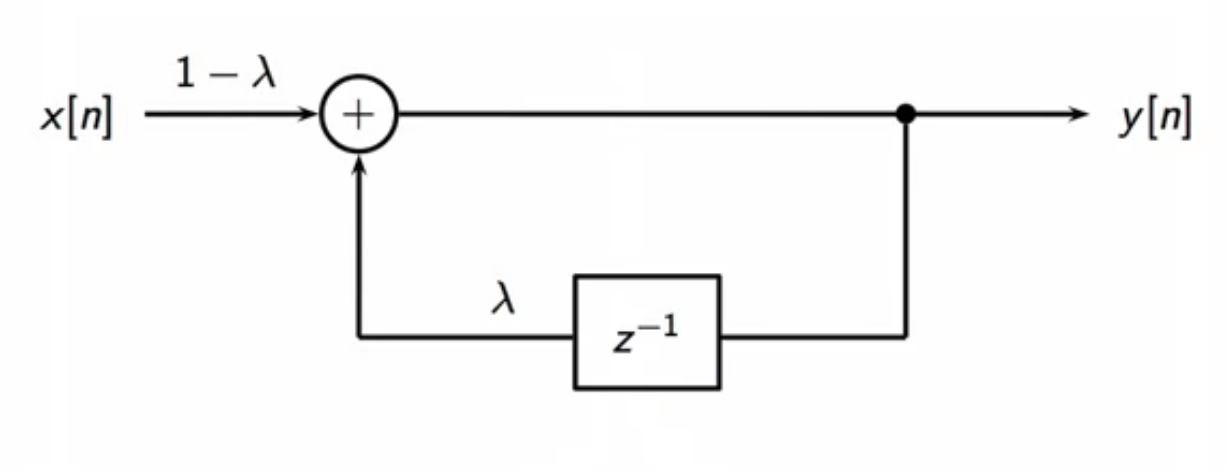
leaky-integrator-filter-struct

fig: leaky-integrator filter structure block diagram

filter equations

\[ \text{leaky-integrator transfer function} \
\begin{align} H(z) & = \frac{(1-\lambda)}{1-\lambda z ^{-1}} \
\
\end{align} \]

\[ \text{leaky-integrator CCDE} \
\begin{align} y[n] & = (1 - \lambda)x[n] + \lambda y[n-1] \
\end{align} \]

zero-pole plot

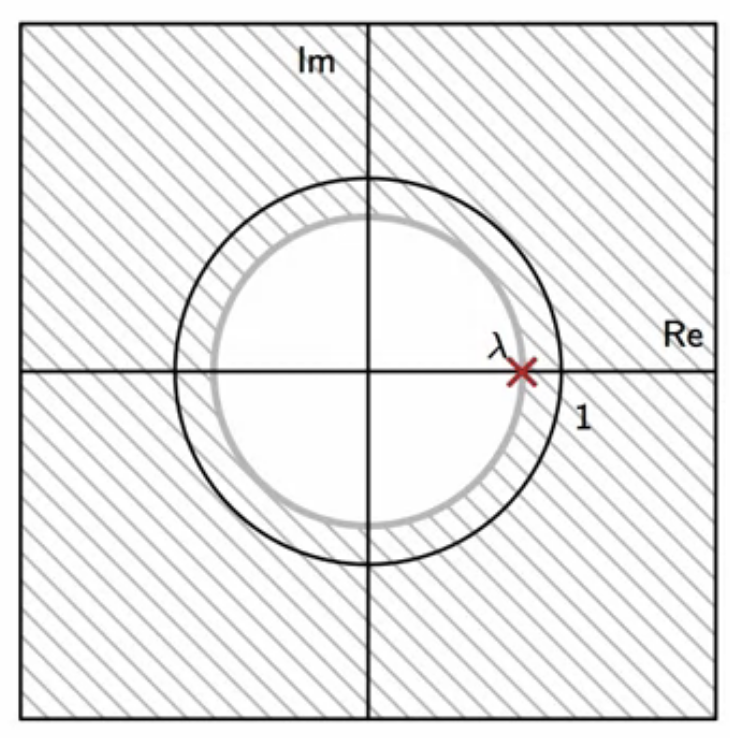
leaky-integrator-zero-pole-plot

fig: leaky-integrator zero-pole plot

  • \(\lambda \) is the only pole in the leaky-integrator zero-pole plot
    • it is a real pole
    • no complex conjugates

frequency domain

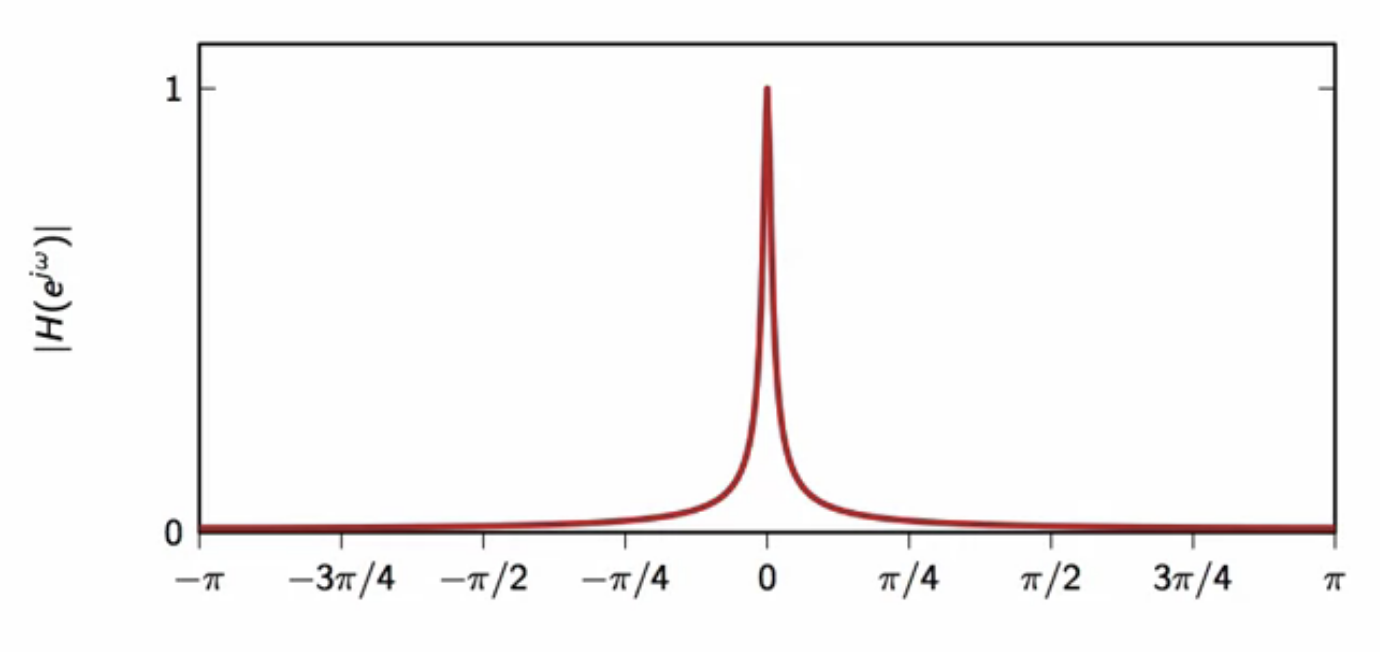
leaky-integrator-freq-resp

fig: leaky-integrator frequency response \(\lambda = 0.98\)

  • gets more concentrated at \(0\) as \(\lambda \) get closer to \(1\)

resonator

  • a resonator is a narrow bandpass filter
    • maybe derived from a leaky integrator
  • filter mechanism is to shift the passband of the leaky-integrator
    • used to detect the presence of a sinusoid at a given frequency
  • useful in communication systems and DTMF (dual-tone-multi-frequency) signals
  • DTMF (dual-tone-multi-frequency) signals
    • used to identify which key has been pressed
    • at the central telephone exchange

zero-pole plot

  • the pole at \(\lambda \) of the leaky integrator
  • generate a complex conjugate pole to make the filter realizable

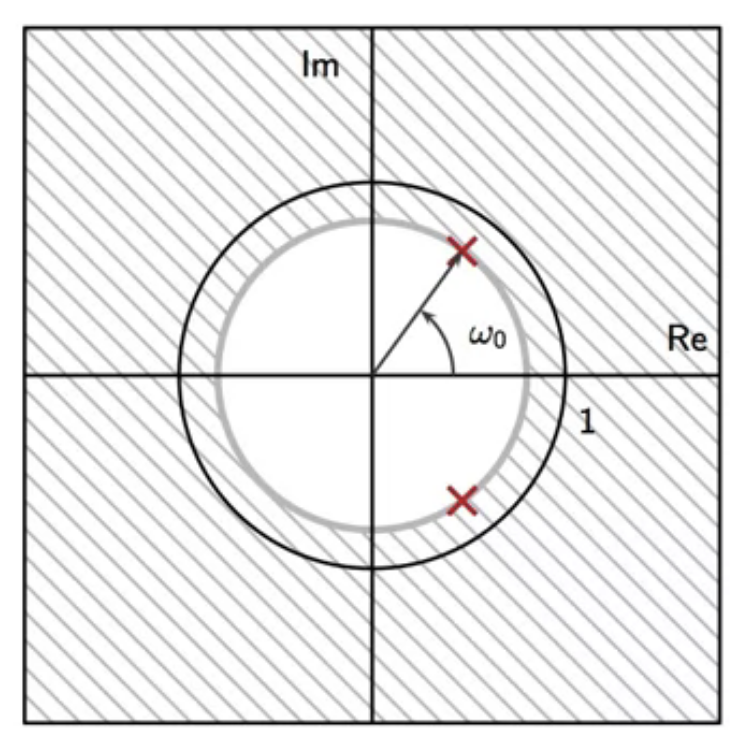
resonator-zero-pole-plot

fig: resonator zero-pole plot (shifted leaky-integrator pole)

  • this shifts the passband
  • may be tuned to the desired frequency \(\omega_0\)

filter block

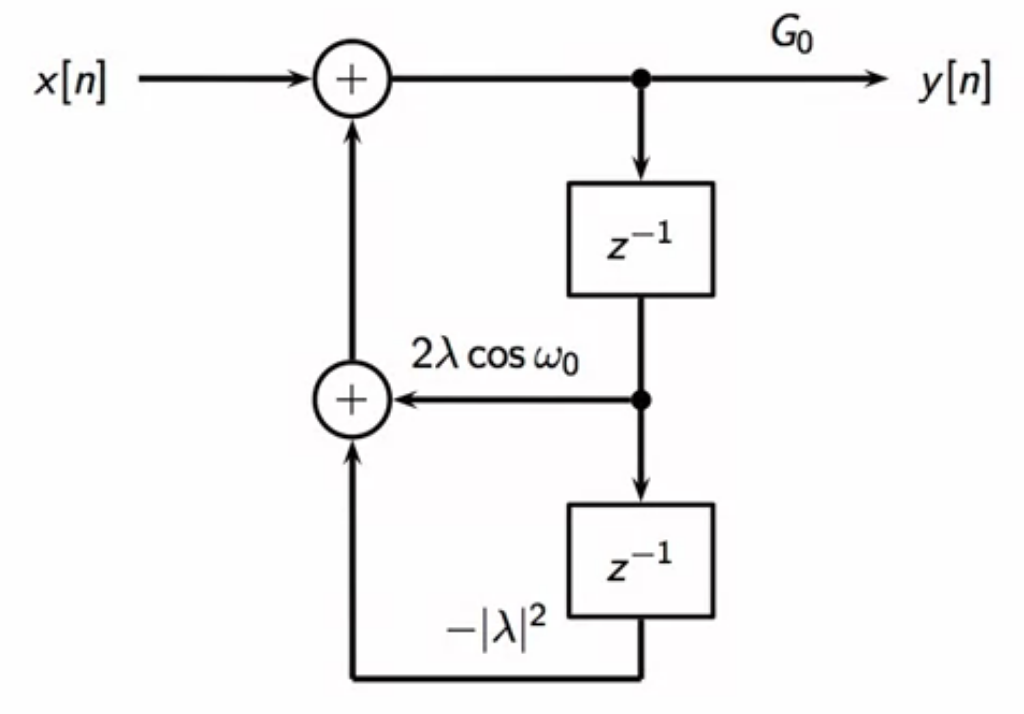
resonator-frequency-response

fig: resonator filter structure block diagram

  • simple second order feedback loop
  • with two delays
    • first delay scaled by one constant
    • first delay scaled by a different constant

filter equations

\[ \text{resonator transfer function} \
\
\begin{align} H(z) & = \frac{G_0}{(1-p z^{-1})(1-p^* z^{-1})} \
\
p & = \lambda e^{j \omega} \
\end{align} \]

\[ \text{resonator CCDE} \
\
\begin{align} y[n] & = G_0 x[n] - a_1 y[n-1] - a_2 y[n-2] \
\
a_1 & = 2 \lambda \cos \omega_0 \
a_2 & = - \vert \lambda \vert ^ 2\
\end{align} \]

frequency response

resonator-frequency-response

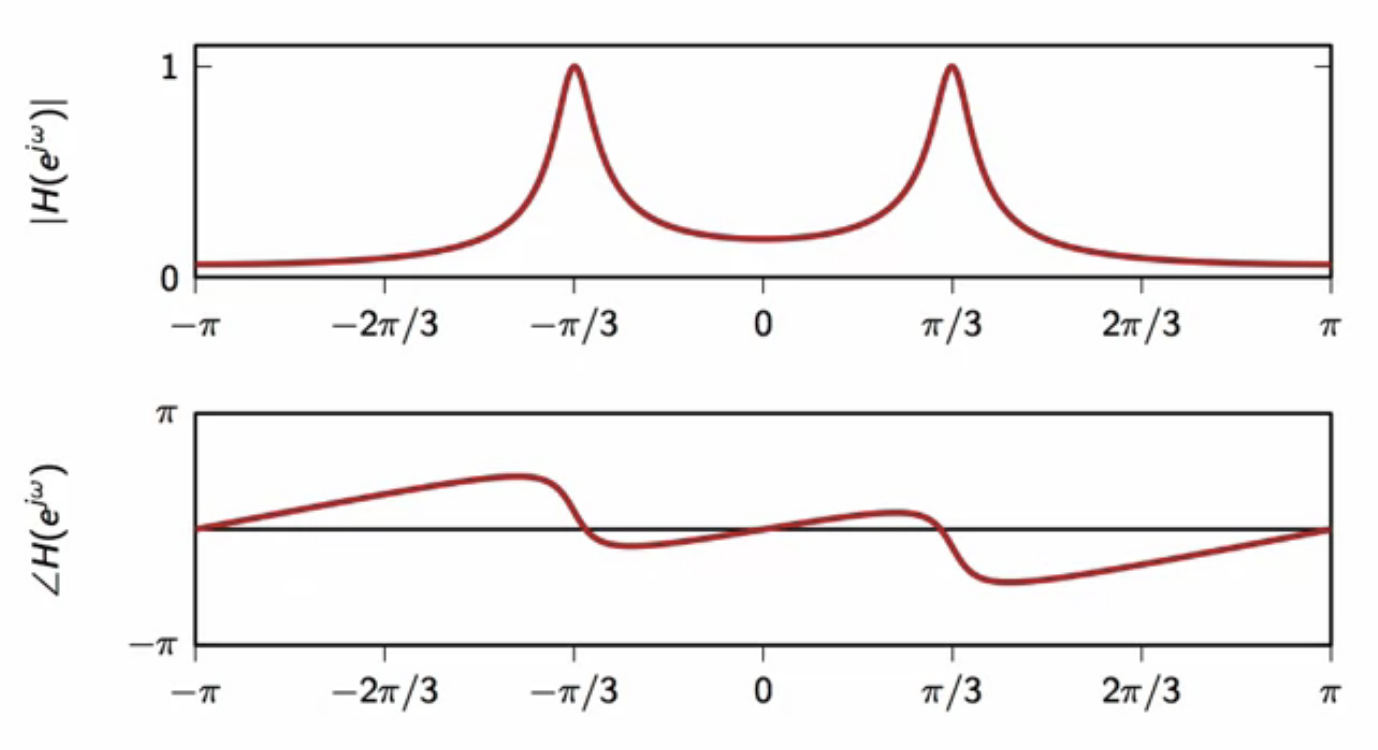
fig: resonator frequency response (\(\omega_0 = \frac{\pi}{3}; \lambda = 0.9\))

  • two peaks centered around \(\omega_0\)
    • here \(\omega_0 = \frac{\pi}{3} \)
  • phase is non-zero
  • not very selective as passband is spread out
    • choose \( \lambda \) closer to \(1\) for more selectivity

DC removal filter

  • DC: direct current

  • a DC balanced signal has zero-mean \[ \lim_{N \rightarrow \infty} \sum_{n = -N}^{N} x[n] = 0 \]
    • no direct current component, i.e. no offset from center
    • its DTFT at zero is zero
  • signals are DC balanced because
    • DC offset doesn’t carry any information
    • but wastes current in circuits
  • a DC removal filter makes a signal DC balanced
    • removes DC bias from a non zero-centered signal
    • by removing frequency component at \(\omega = 0 \)

zero-pole plot

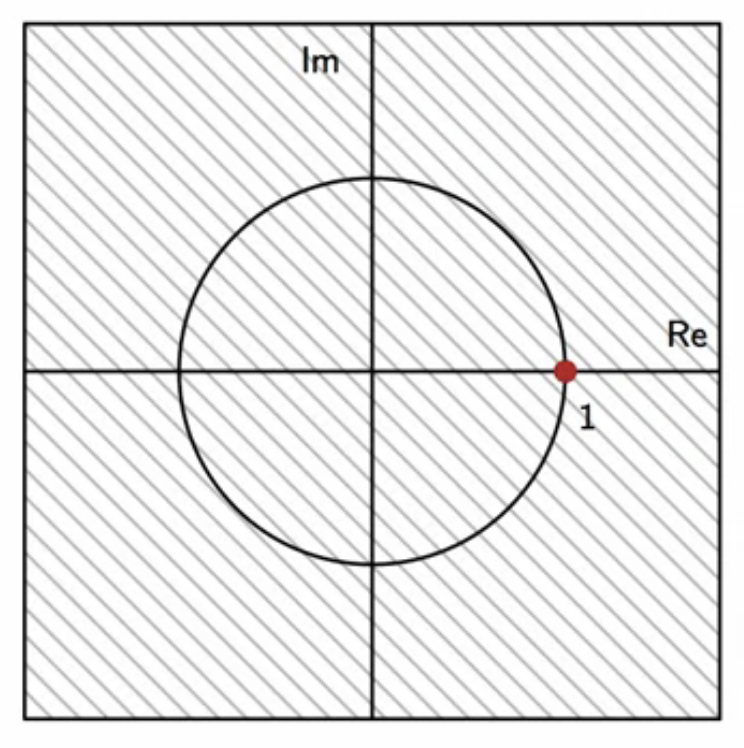
dc-removal-zero-pole-plot

fig: DC removal filter zero-pole plot

  • place zero at \(z = 1\)
    • point on complex plane where \(\omega = 0\)

filter equations

\[ \text{DC removal filter transfer function} \
\
\begin{align} H(z) & = 1 - z^{-1} \
\
\end{align} \]

\[ \text{DC removal filter CCDE} \
\
\begin{align} y[n] & = x[n] - x[n-1] \
\
\end{align} \]

frequency response

dc-removal-frequency-response

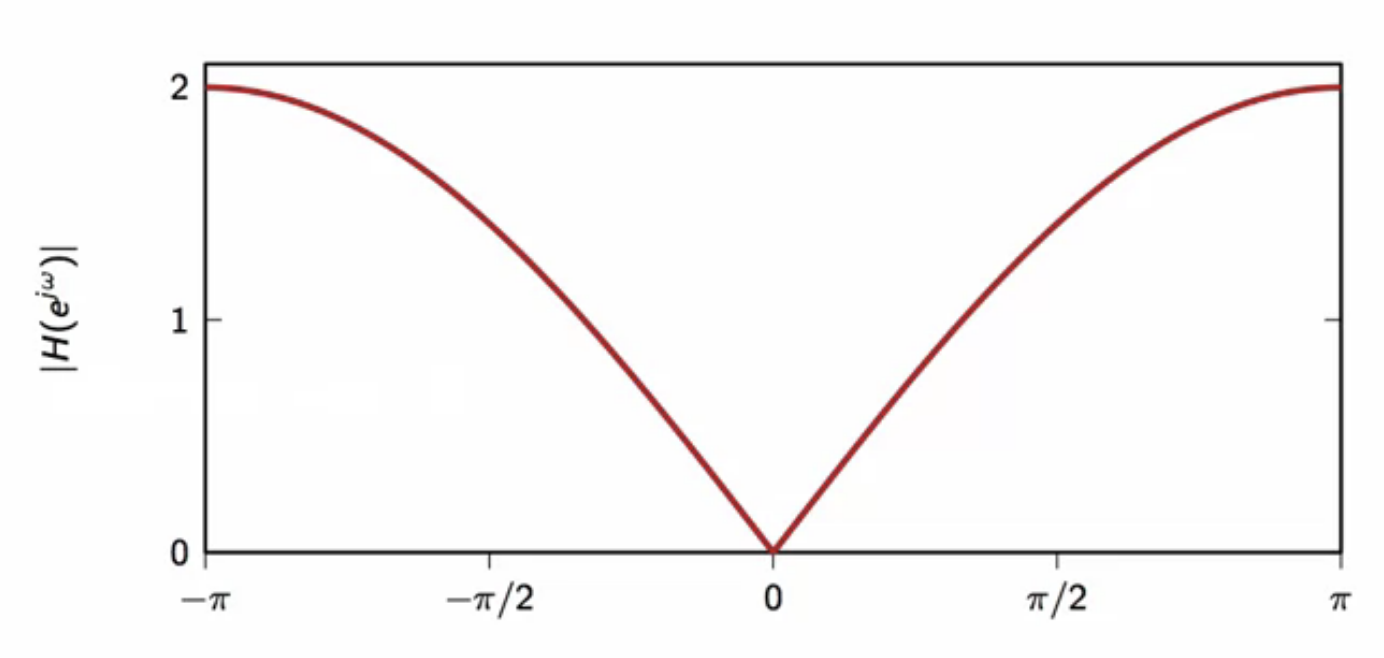
fig: DC removal filter frequency response

  • frequency component at \( \omega = 0 \) is \(0 \)
  • but the response introduces an attenuation in surrounding frequencies
    • in almost the entire response in \([-\pi,\pi] \)
    • which is not acceptable
  • a notch behavior design is needed to avoid this
    • DC notch filter is explored

DC Notch

  • to avoid undesired attenuation in frequencies
    • surrounding \( \omega = 0 \)
    • in almost the entire response in \([-\pi,\pi] \)
    • DC removal filter design needs ot be improved
  • going back to the circus-tent method, the zero-pole plot of the DC removal filter is modified

zero-pole plot

  • in the DC removal filter zero-pole plot
    • a pole pushes up the frequency response magnitude, while a zero pushes it down
    • so a pole is added close to the center, inside the unit circle
    • the location of the pole is given by \(\lambda \)
      • like the pole of the leaky-integrator zero-pole plot

dc-notch-zero-pole-plot

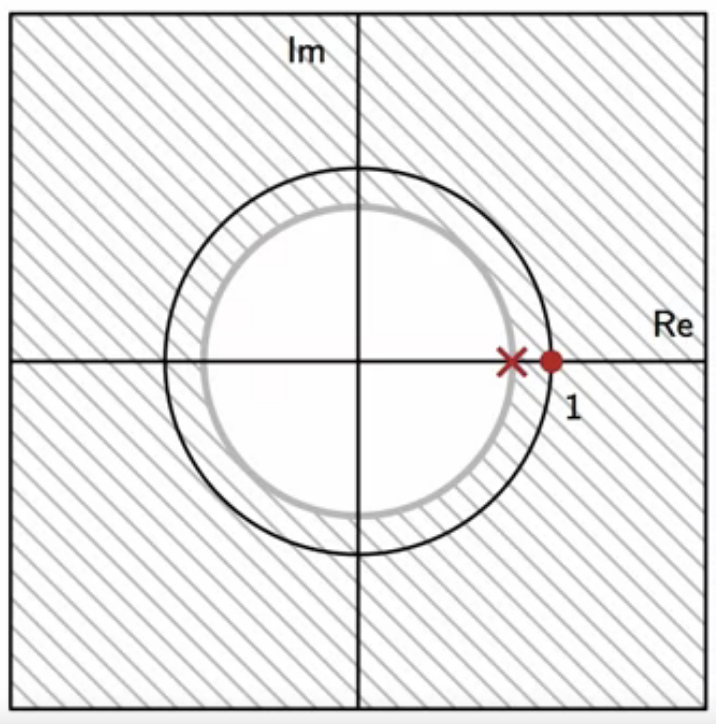
fig: DC notch zero-pole plot

  • this is a combination of a DC removal zero at \( 1 \) and
    • a leaky-integrator pole

filter equations

\[ \text{DC notch transfer function} \
\
\begin{align} H(z) & = \frac{1-z^{-1}}{1 - \lambda z^{-1}} \
\
\end{align} \]

\[ \text{DC notch filter CCDE} \
\
\begin{align} y[n] & = \lambda y[n-1] + x[n] - x[n-1] \
\
\end{align} \]

frequency response

dc-notch-frequency-response

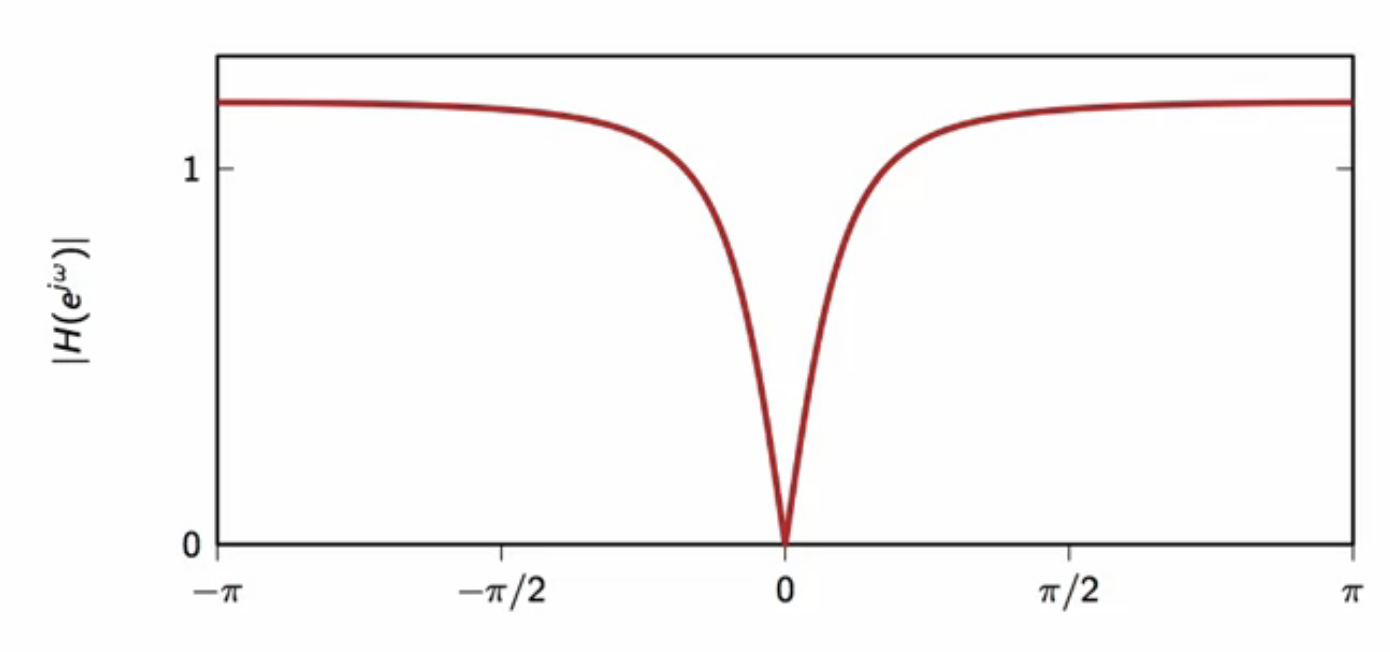
fig: DC notch frequency response \( \lambda = 0.7 \)

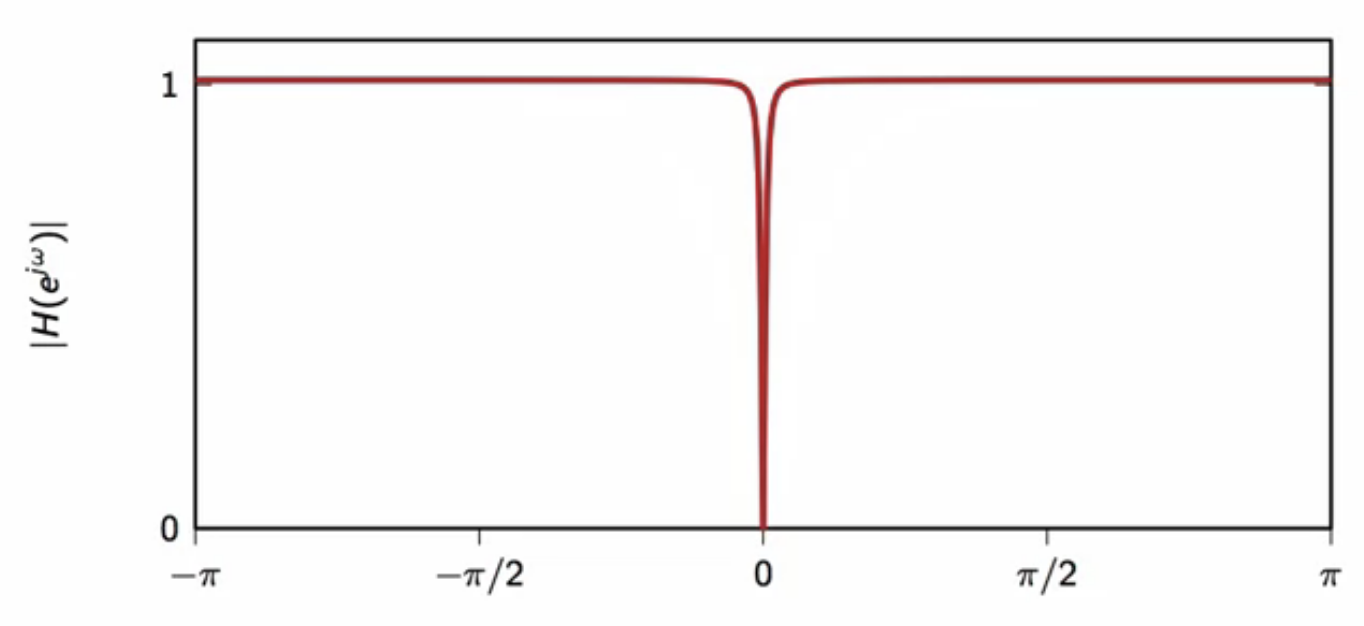
dc-notch-frequency-response-sharper

fig: DC notch frequency response \( \lambda = 0.98 \)

  • as \( \lambda \) gets closer to \(1\)
    • filter notch gets very narrow
  • width of frequency attenuation may be tuned with \(\lambda \)

filter block

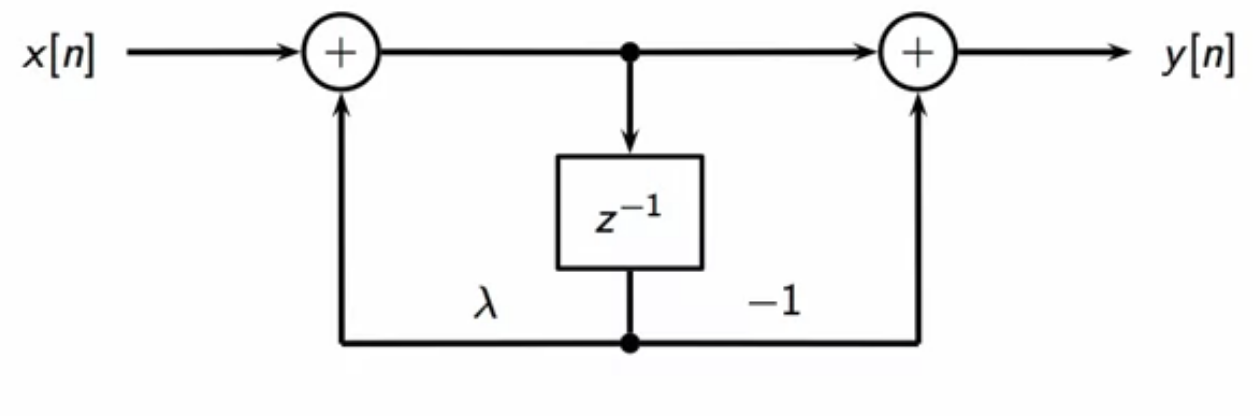
dc-notch-struct-block

fig: resonator filter structure block diagram

  • delay is shared between feedforward and the feedback loop

hum removal

  • a filter derived from DC notch
  • a DC notch removed frequencies only at \(\omega = 0\)
    • hum removal shifts the notch to remove a non-zero frequency
  • useful in the music studio
  • amplifiers pick up the hum from the electric mains
    • 50Hz - europe
    • 60HZ - north america
  • this may be removed with a hum removal filter

zero-pole plot

  • the hum removal strategy is similar to deriving a resonator from a leaky-integrator
    • the real pole of the leaky is moved to complex conjugate ones
    • this shifts the passband central frequency
    • resulting in a resonator
  • similarly, the real pole of the DC notch is moved to complex complex ones
    • the notch central frequency moves to a non-zero with this act
    • the resulting filter is called a hum remover
    • as its popular application is removing hum from electrical instruments
  • the real zero of the DC notch is moved to complex conjugate ones

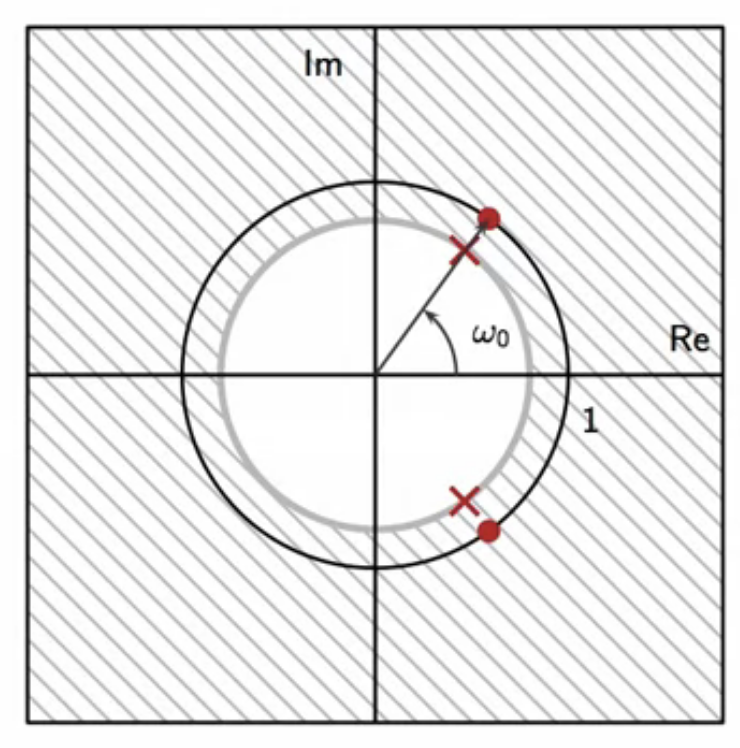
hr-zero-pole-plot

fig: hum removal zero-pole plot

filter equations

\[ \text{hum removal transfer function} \
\
\begin{align} H(z) & = \frac{ ( 1 - e^{j \omega_0} z^{-1} ) (1 - e^{-j \omega_0} z^{-1} ) }{ (1 - \lambda e^{j \omega_0} z^{-1}) (1 - \lambda e^{-j \omega_0} z^{-1}) } \
\
\end{align} \]

frequency response

hum-removal-frequency-response

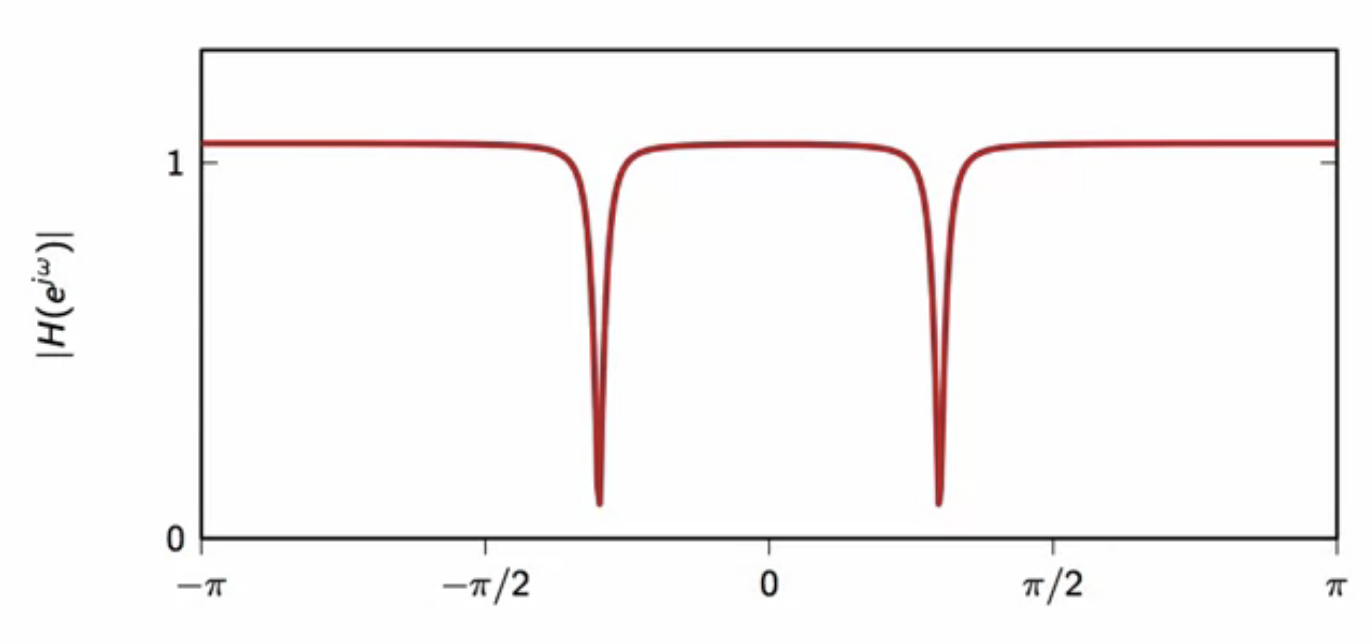
fig: hum removal frequency response \( \lambda = 0.95 \)

  • notches at \(\omega_0 \leq = 0\)
  • removes frequency component at \( \omega_0 \)

filter block

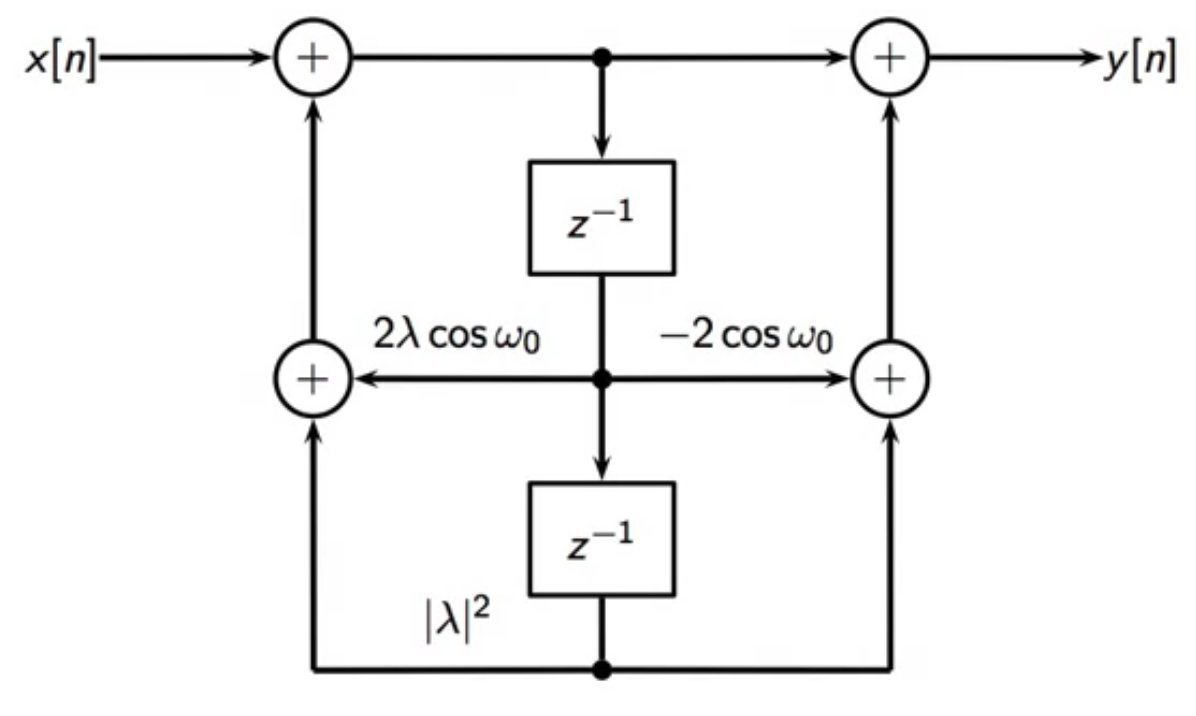
hum-removal-struct-block

fig: hum removal filter structure block diagram

  • two delay stages
    • each scaled differently
  • delay is shared between feedforward and the feedback loop

references