[DSP] W07 - Continuous-Time

contents

• continuous-time
  • analog world
  • discrete world
  • analog-analog conversions
  • digital-analog conversions
  • analog-digital conversions
  • conversion cycle
  • continuous-time dsp
  • bandlimited functions
  • example - continuous-time fourier transform

---

continuous-time

• the physical world is assumed to be continuous-time
  • analog is continuous-time
• the computer world is discrete-time

fig: continuous-time world vs. discrete-time world metaphor

analog world

• calculus
• distributions
• systems theory

• electronics

• mathematical parallel:
  • real-values time: $t$ (sec)
  • functions: $x\left(t\right)\in L_2\left(R\right)$
  • frequency: $\Omega \in R\left(\frac{rad}{sec}\right)$
    • unlimited, not bound
  • fourier-transform: $L_2\left(R\right)\mapsto L_2\left(R\right)$

discrete world

• arithmetic
• combinatorics
• computer science

• dsp

• mathematical parallel:
  • countable integer index: $n$
  • sequences: $x\left[n\right]\in {\ell }_2\left(Z\right)$
  • frequency: $\omega \in [-\pi ,\pi ]$
    • bounded
  • dtft: ${\ell }_2\left(Z\right)\mapsto L_2\left(\right[-\pi ,\pi \left]\right)$

analog-analog conversions

• dsp is used for analog-analog transform with intermediate digital processing
• example:
  • mp3
  • digital photography
• process input $x\left(t\right)$ and output $y\left(t\right)$ are both continuous-time
• process intermediate processing in on discrete sequences $x\left[n\right],y\left[n\right]$
• usually a storage, transport and reproduction process

digital-analog conversions

• there can be conversion from discrete-time to analog-time done with dsp
• examples:
  • computer graphics
  • video games
• process input $x\left[n\right]$ is discrete-time
• process output $y\left(t\right)$ is continuous-time

• intermediate processing in on discrete sequences $x\left[n\right],y\left[n\right]$

• usually a synthesis process

analog-digital conversions

• there can be conversion from discrete-time to analog-time done with dsp
• examples:
  • control systems
  • measurement systems
  • surveillance applications
• process input $x\left(t\right)$ is continuous-time
• process output $y\left[n\right]$ is discrete-time

• intermediate processing in on discrete sequences $x\left[n\right],y\left[n\right]$

• usually a monitoring and reactive process

conversion cycle

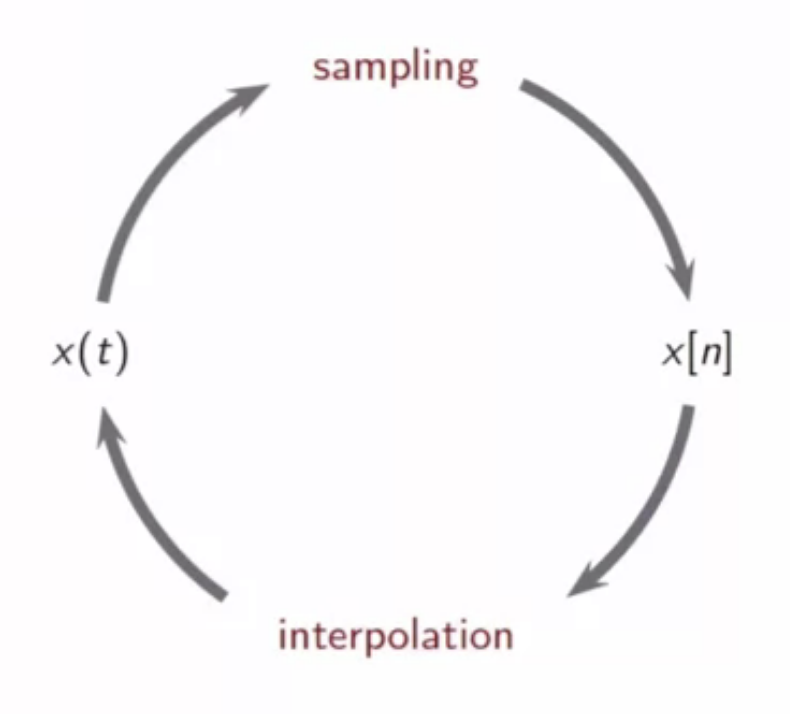
fig: $x\left(t\right)$ - continuous-time; $x\left[n\right]$ - discrete-time

continuous-time dsp

• time: real variable $t$
• signal $x\left(t\right)$ - complex function of a real variable
• finite energy: $x\left(t\right)\in L_2\left(R\right)$
• inner product in $L_2\left(R\right)$ $$⟨x\left(t\right),y\left(t\right)⟩={\int }_{-\infty }^{\infty }{x}^{\ast }\left(t\right)y\left(t\right)dt$$
• energy: $$\left|\right|x\left(t\right)|{|}^2=⟨x(t),x(t)⟩$$
• fourier-transform: $L_2\left(R\right)\mapsto L_2\left(R\right)$

analog LTI filters

fig: block diagram of an analog LTI

• these are the analog parallel of discrete LTI filters

• here, $$\begin{array}{cc}y\left(t\right)& =(x\ast h)\left(t\right)\\ & =⟨h^{\ast }(t-\tau ),x\left(\tau \right)⟩\\ & ={\int }_{\infty }^{\infty }x\left(\tau \right)h(t-\tau )d\tau \end{array}$$

continuous-time fourier transform (CTFT)

• in discrete-time max angular frequency is $\pm \pi$
• in continuous-time no upper bound to frequency $\omega \in R$
• however, the concept of breaking a function down into component sines is still the same $$\begin{array}{ccc}& \text{forward fourier-transform}& \\ X\left(j\Omega \right)& ={\int }_{\infty }^{\infty }x\left(t\right)e^{-j\Omega t}dt& \leftarrow \text{not periodic}\\ & & \\ & \text{inverse fourier-transform}& \\ x\left(t\right)& =\frac{1}{2\pi }{\int }_{\infty }^{\infty }X\left(j\Omega \right)e^{j\Omega t}d\Omega & \end{array}$$

real-world frequency

• $\Omega$ is expressed in $\frac{rad}{s}$
• $F=\frac{\Omega }{2\pi }$ expressed in Hertz $\left(\frac{1}{s}\right)$
• period $T=\frac{1}{F}=\frac{2\pi }{\omega }$

example

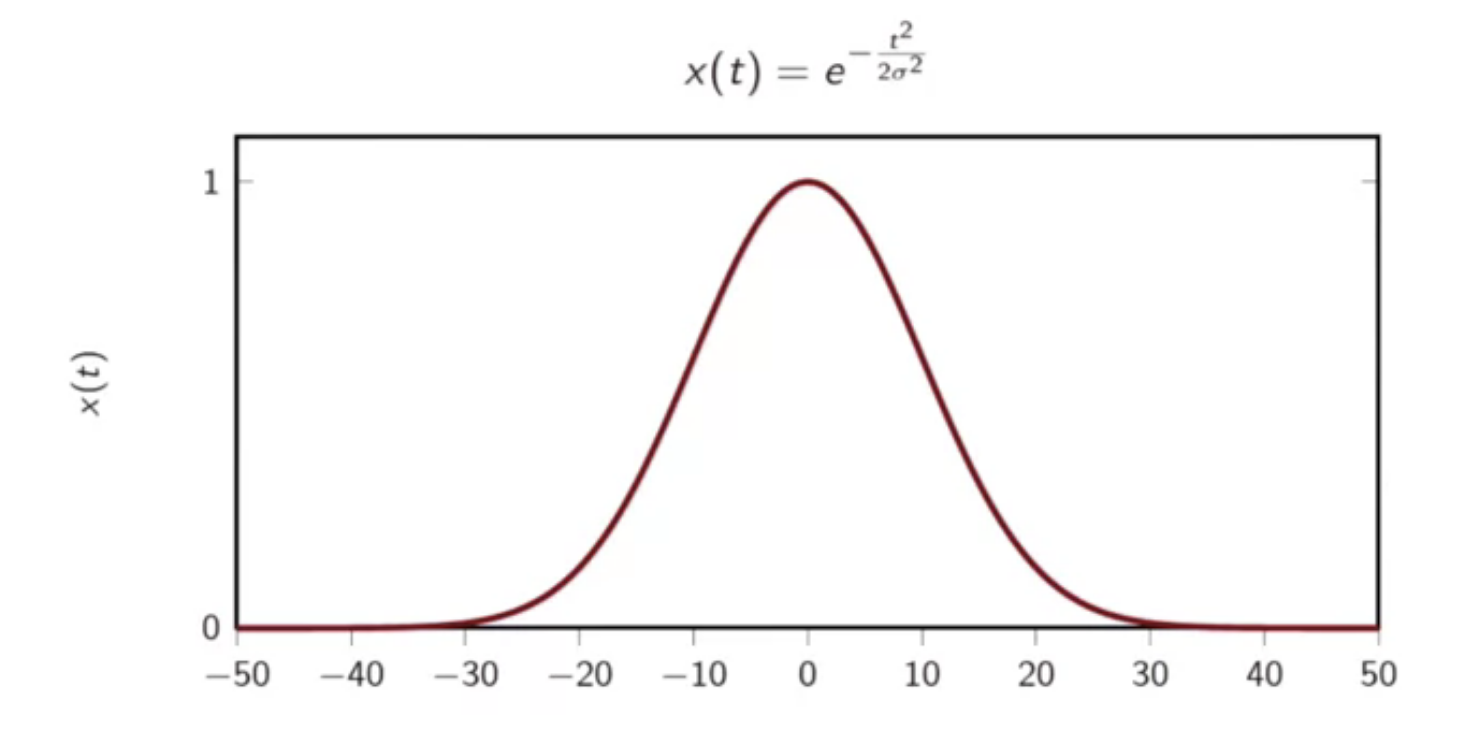
fig: gaussian signal (analog)

• the fourier transform of above gaussian signal as a bell shaped magnitude curve
  • rescaled appropriately

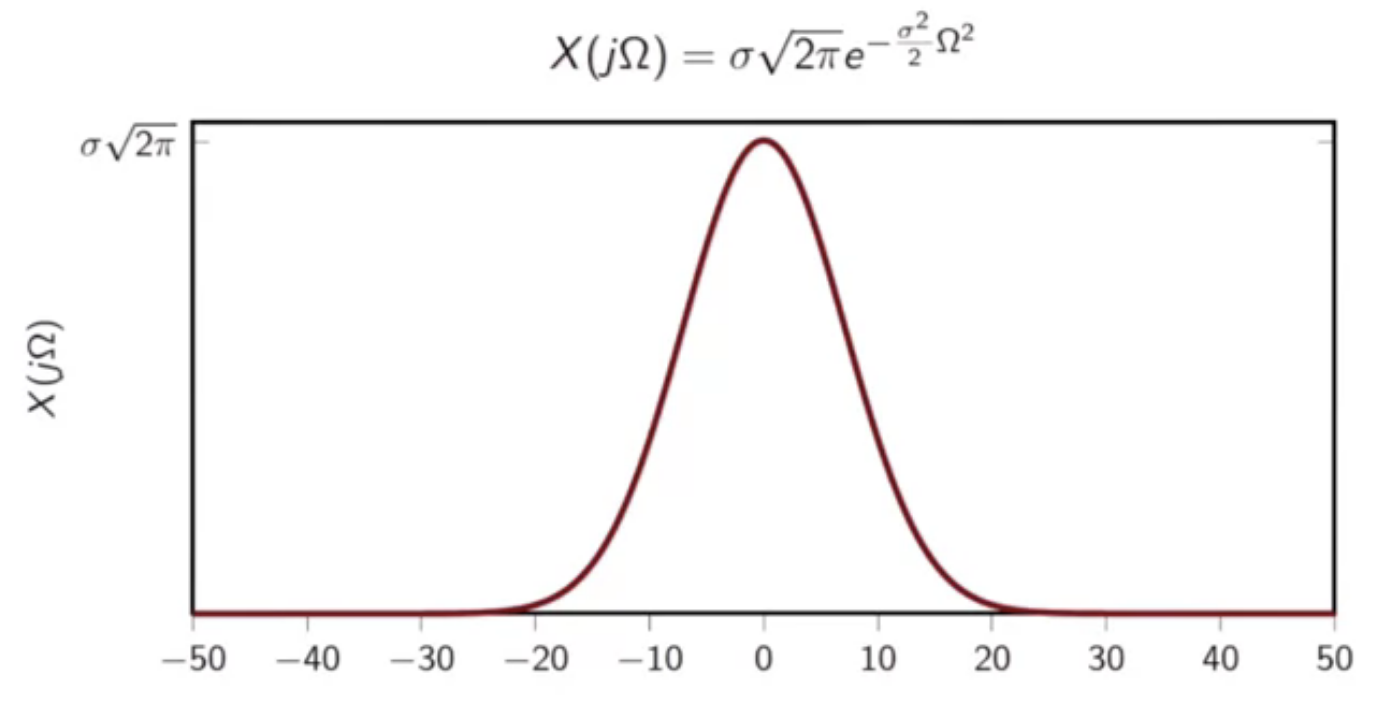
fig: gaussian signal fourier transform magnitude

continuous-time convolution

• for following filter action

fig: block diagram of an analog LTI

• the filter output fourier transform is scaling the input fourier transform with the frequency response of the filter
  • frequency response is nothing but the fourier transform of the filter impulse response

$$Y\left(j\Omega \right)=X\left(j\Omega \right)H\left(j\Omega \right)$$

bandlimited functions

• ${\Omega }_N$-bandlimitedness $$X\left(j\Omega \right)=0\text{for}\left|\Omega \right|>{\Omega }_N$$

example - continuous-time fourier transform

• a bandlimited rect function

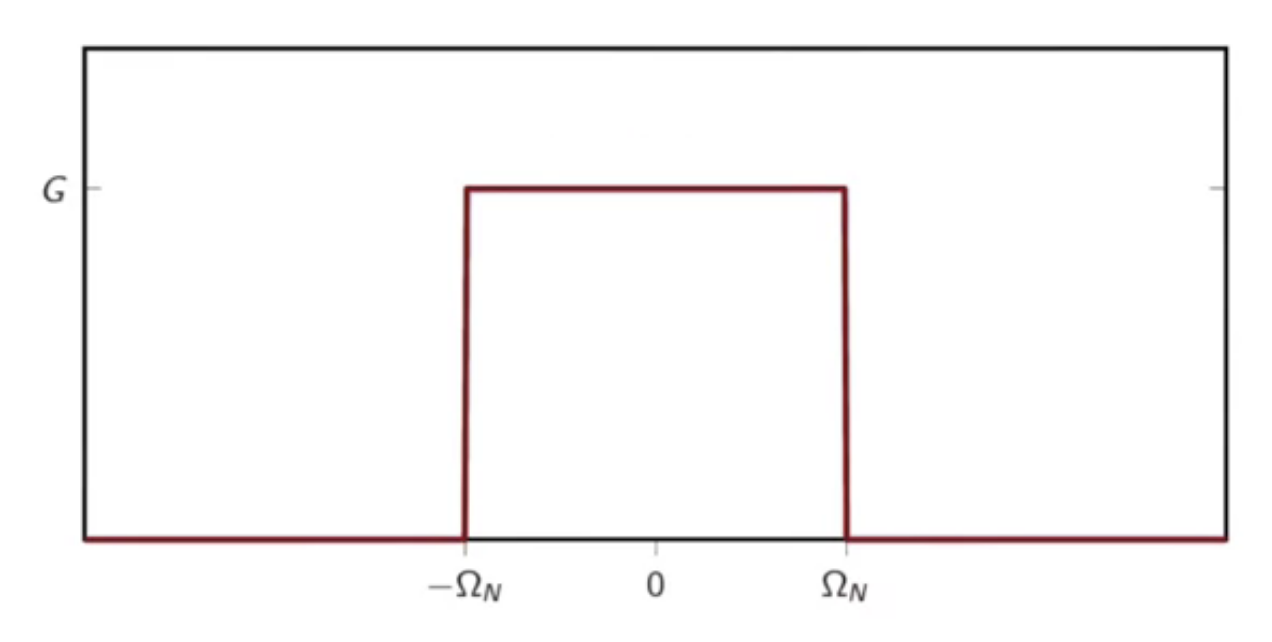
fig: prototypical bandlimited function

fourier transfer

$$\begin{array}{cc}\Phi \left(j\Omega \right)& =Grect(\frac{\Omega }{2{\Omega }_N})\\ \phi \left(t\right)& =G\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\varphi \left(j\Omega \right)e^{j\Omega t}d\Omega \\ & =G\frac{{\Omega }_N}{\pi }sinc(\frac{{\Omega }_N}{\pi }t)\end{array}$$

• normalization: $G=\frac{\pi }{{\Omega }_N}$
• total bandwidth: ${\Omega }_B=2\pi {\Omega }_N$
• define: $T_s=\frac{2\pi }{{\Omega }_B}=\frac{\pi }{{\Omega }_N}$

fig: prototypical bandlimited function

• with define substitutions $$\begin{array}{cc}\Phi \left(j\Omega \right)& =\frac{\pi }{{\Omega }_N}rect(\frac{\Omega }{2{\Omega }_N})\\ \phi \left(t\right)& =sinc(\frac{t}{T_s})\end{array}$$

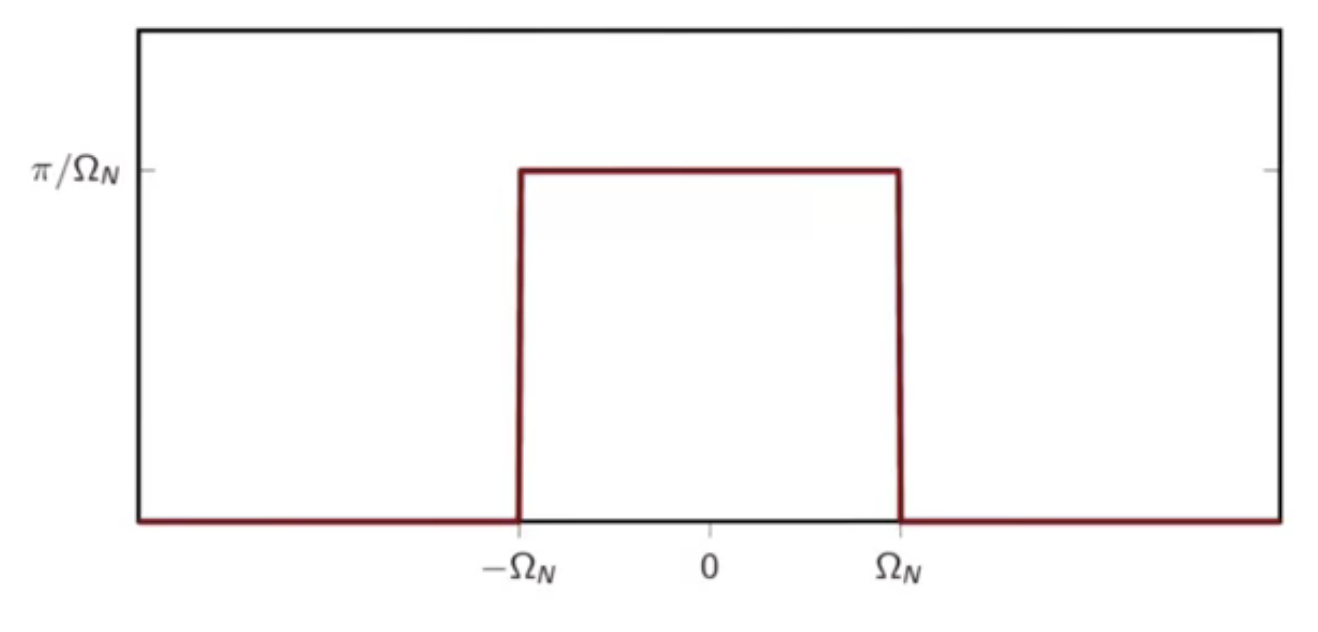
fig: prototypical bandlimited function with substitution

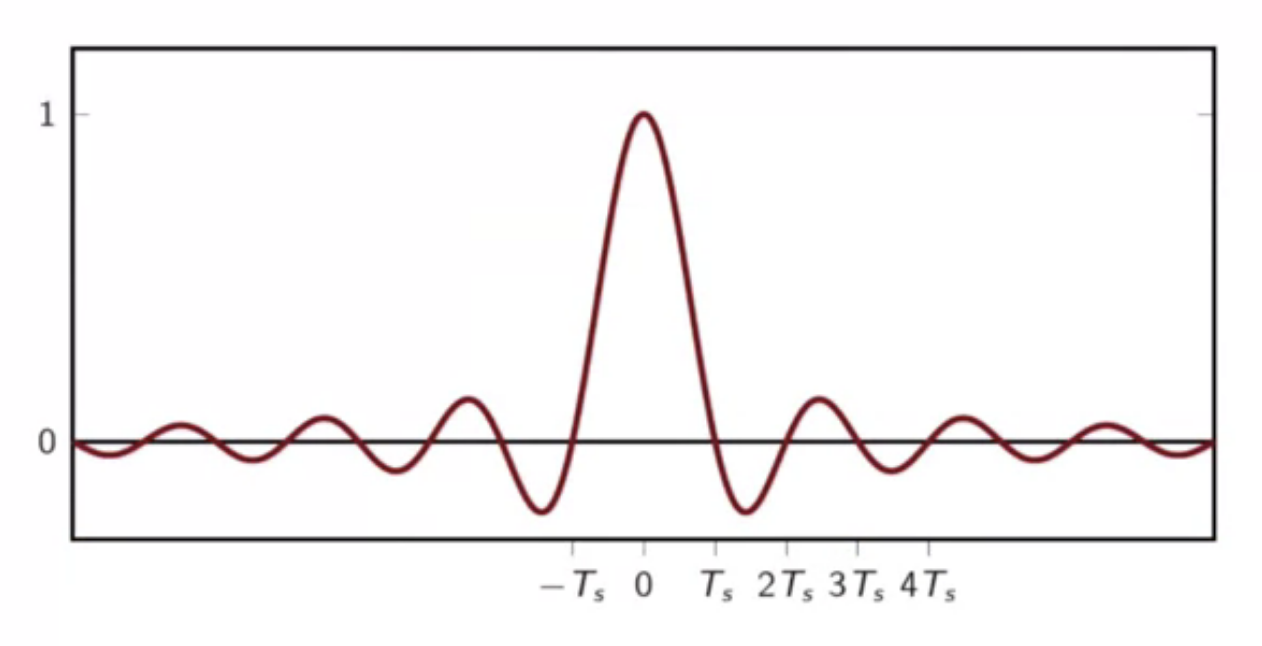
fig: fourier transform of prototypical bandlimited function

---

references

• ecole dsp - filters