contents

  • the first half of dsp is the discretisation of time, i.e., sampling.
  • the second half is quantization
  • digital devices can only deal with integers no matter how many bits are used
  • so, the numeric range of the finite samples has to mapped on to a set of finite values
    • in doing so, there is an irreversible loss of information
    • the quantizer introduces noise

stochastic signal processing

  • stochastic: random
  • random signals need processing in the real-world
  • deterministic signals are known in advance
  • many interesting signals are known in advance
    • only a few things about it are known
    • eg: speech signal
  • stochastic signals are described probabilistically
  • such random signals can be dsped as well

single discrete-time random signal generator

  • a fair coin toss \[ x[n] = \Bigg{ \begin{matrix} +1 & \text{ n-th toss is head } \ -1 & \text{ n-th toss is tail } \end{matrix} ]
  • each sample is independent of the other
  • each sample has 50% probability
  • each time the generator is run, the signal is realized differently
  • the mechanism behind each instance is know
  • but that particular realization is not known before hand
  • this can be analyzed spectrally

DFT of a random signal

  • explore DFT of finite set of samples of a random signal
  • every time the experiment is repeated, the result is different
  • longer realizations may be experimented with
averaging
  • when faced with random data, an intuitive approach is to take “averages”
  • in probability theory the average is across different realizations of the experiment, not across the time axis
    • this is called the expectation (E[x[n]])
  • for the coin-toss signal \[ \begin{align} E[x[n]] & = -1 P[\text{n-th toss is tail}] + 1 P[\text{n-th toss is head}]
    & = 0
    \end{align} ]
  • so the average value for each sample is zero
  • so averaging the DFT values will not work as (E[x[n]] = 0)
  • however, the signal does move, so it;s energy or power must be non-zero

random energy and power

  • the coin toss signal has infinite energy [ \begin{align} E_x & = \lim_{N \rightarrow \infty } \sum_{n = -N}^{N} \vert x[n] \vert^2 _
    & = \lim{N \rightarrow \infty } (2N + 1)
    & = \infty
    \end{align} ]
  • power is finite over an interval [ \begin{align} P_x & = \lim_{N \rightarrow \infty } \frac{1}{2N + 1} \sum_{n = -N}^{N} \vert x[n] \vert^2
    & = 1
    \end{align} ]

power spectral density

  • try to average DFT square magnitude, normalized
    • pick an interval length (N)
    • pick a number of iterations (M)
    • tun the signal generator (M) times
      • to obtain ( M ) (N)-point realizations
    • compute the DFT of each realization
    • average their square magnitude divided by (N)
  • this yields the following results

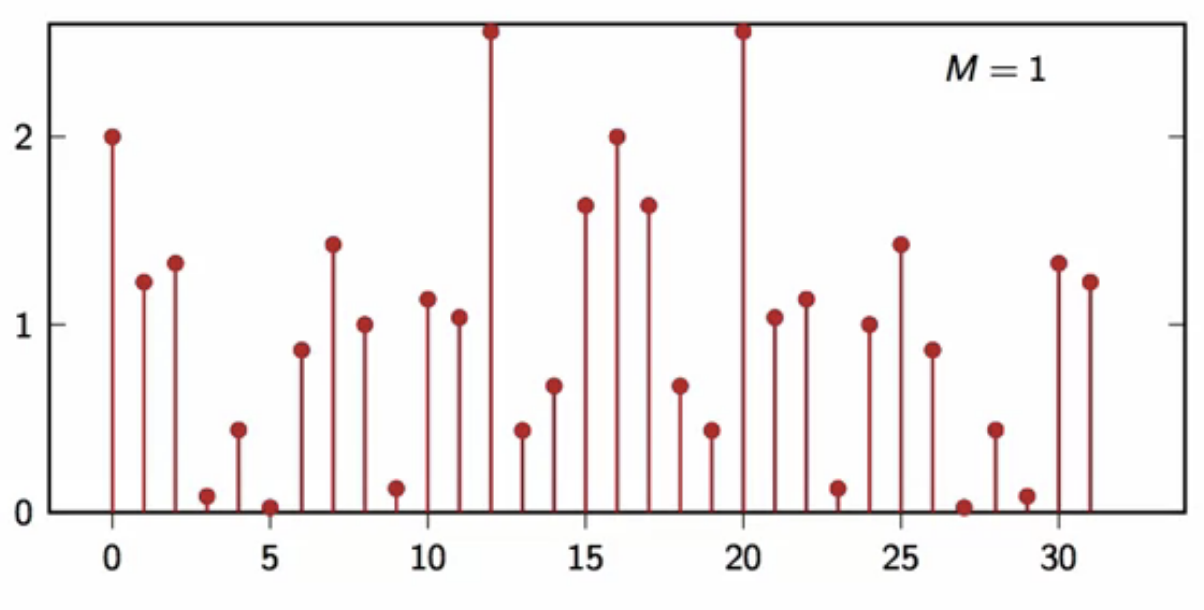
DFT-random-signal-avg

fig: DFT average plot (M = 1)

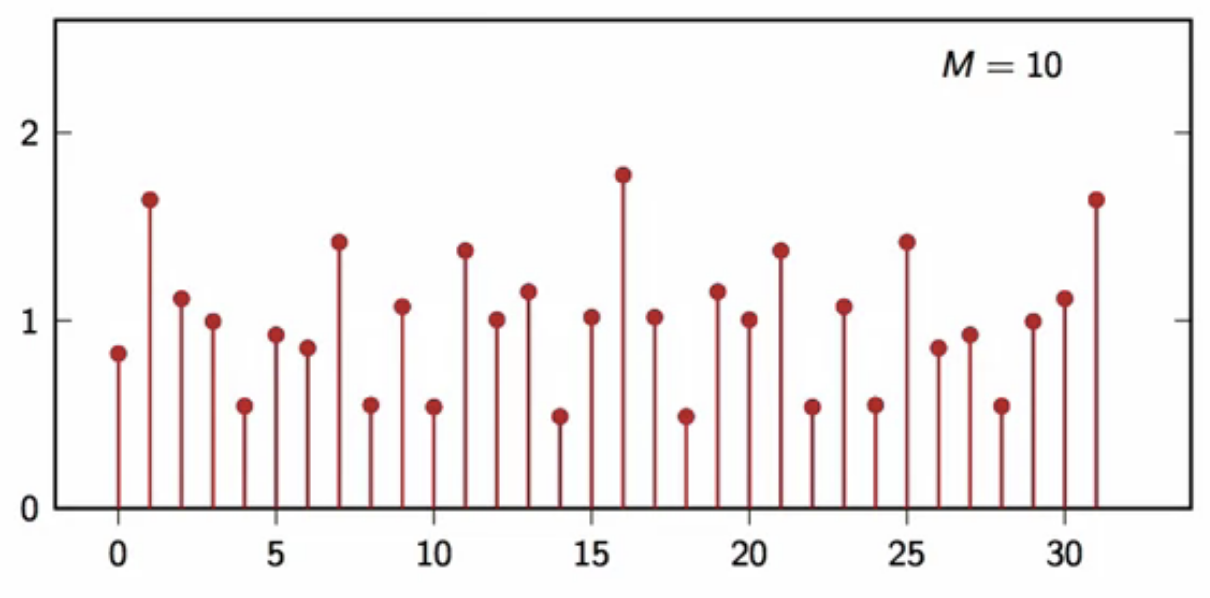
DFT-random-signal-avg

fig: DFT average plot (M = 10)

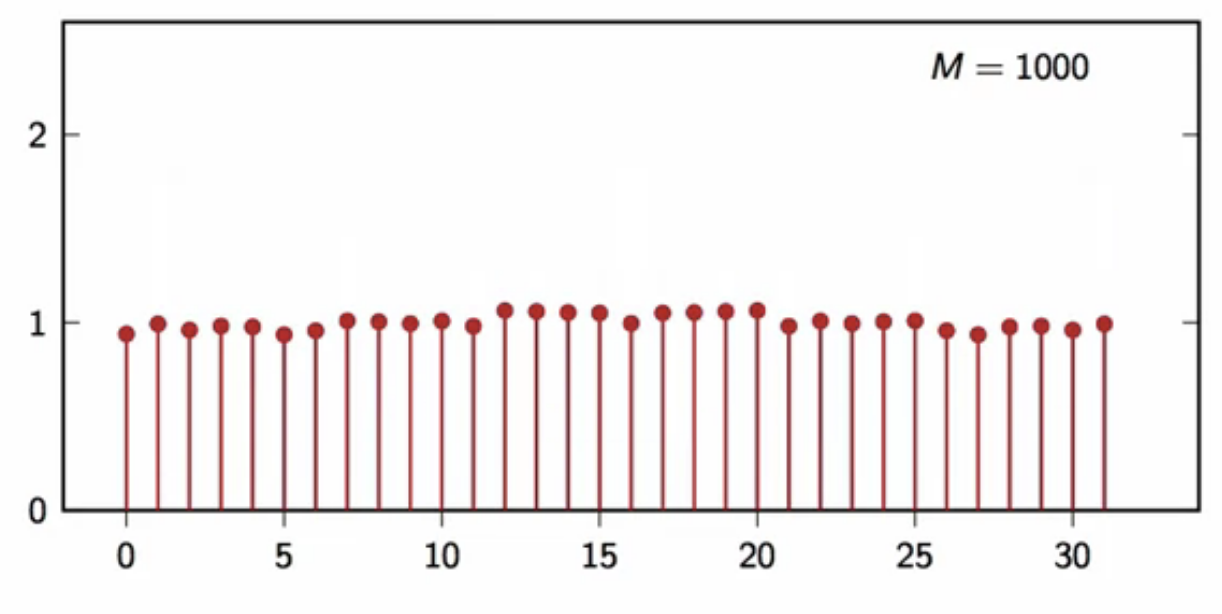
DFT-random-signal-avg

fig: DFT average plot (M = 1000)

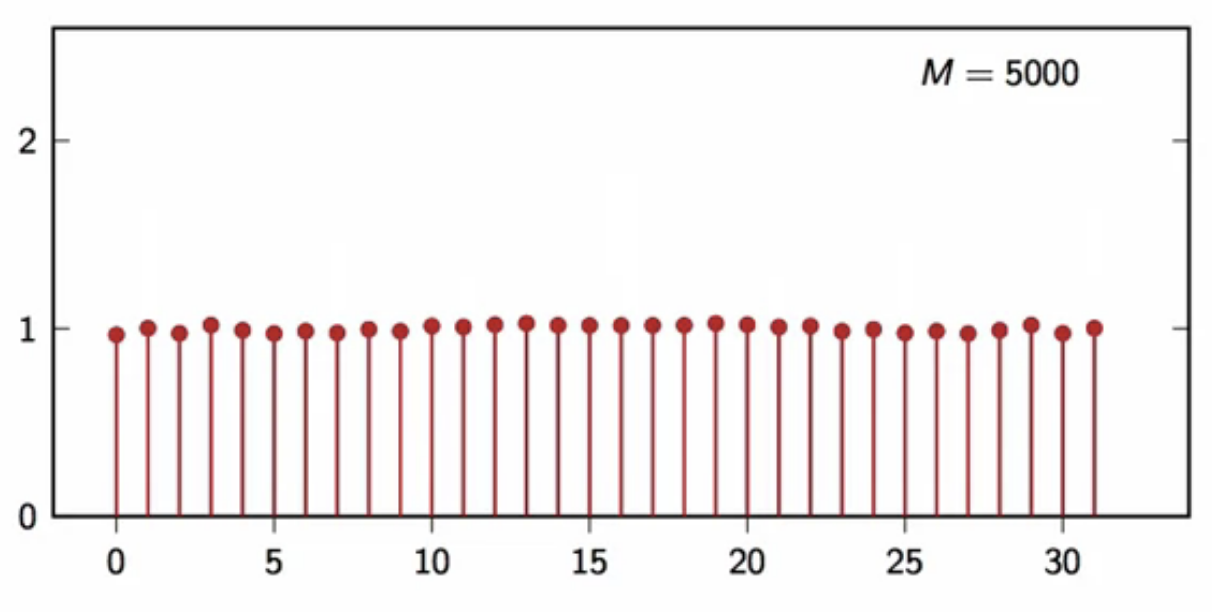
DFT-random-signal-avg

fig: DFT average plot (M = 5000)

  • this is the definition of the power spectral density \[ P[k] = E[\frac{\vert X_N[k]\vert^2}{N}] ]
  • this looks very much like (P[k] = 1)
  • if (\vert X_N[k]\vert^2) tends to the energy distribution in frequency
    • (\frac{\vert X_N[k]\vert^2}{N}) tends to the power distribution
    • i.e. density in frequency
  • the frequency-domain representation for stochastic process is the power spectral density

intuition

  • (P[k]=1) means that power is equally distributed over all frequencies
  • i.e. we cannot predict if the signal moves ‘slow’ or ‘suprfast’
  • this is because each sample is independent of the others
  • a given realization could
    • be all ones
    • or the sign changes alternate sample
    • or anything in between
  • this is also the description of “luck”

filtering a random signal

  • consider a 2-pt moving average filter \[ y[n] = \frac{(x[n] + x[n-1]}{2} ]
  • a random signal (x[n] ) is filtered with this
  • following is the power spectral density of the output of this filter

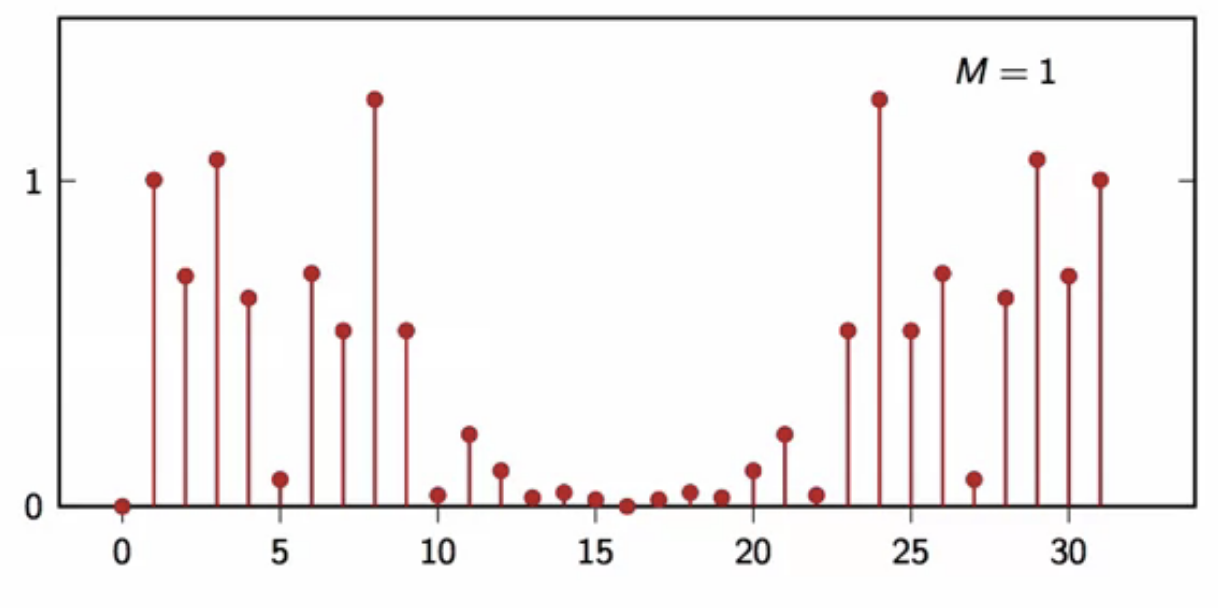
DFT-random-signal-avg

fig: moving average filtered output DFT average (M = 1)

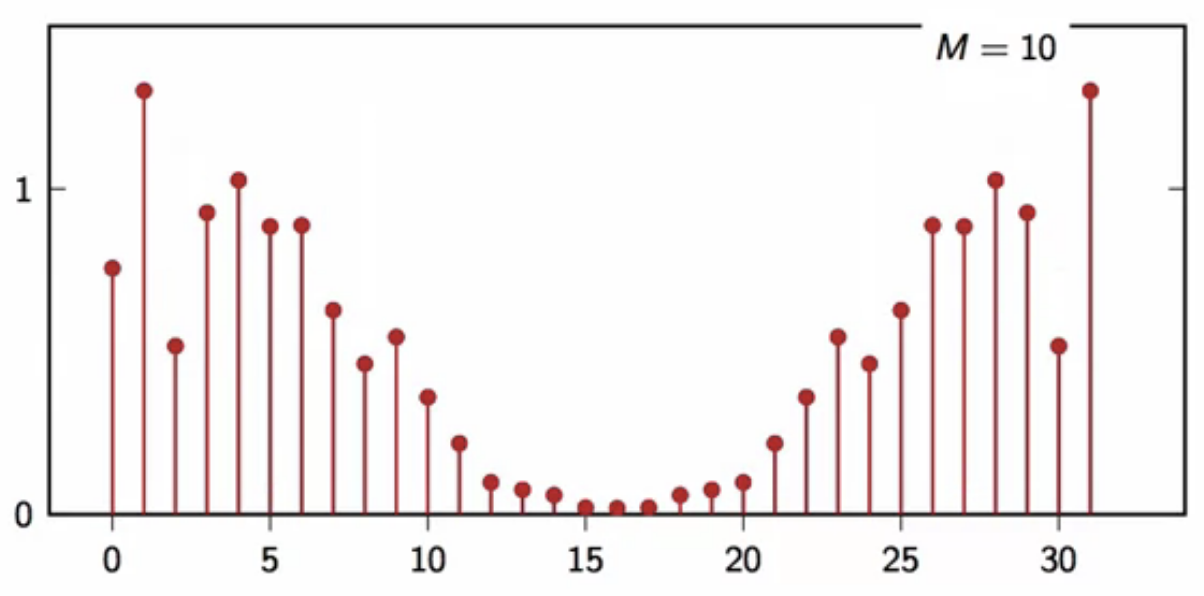
DFT-random-signal-avg

fig: moving average filtered output DFT average (M = 10)

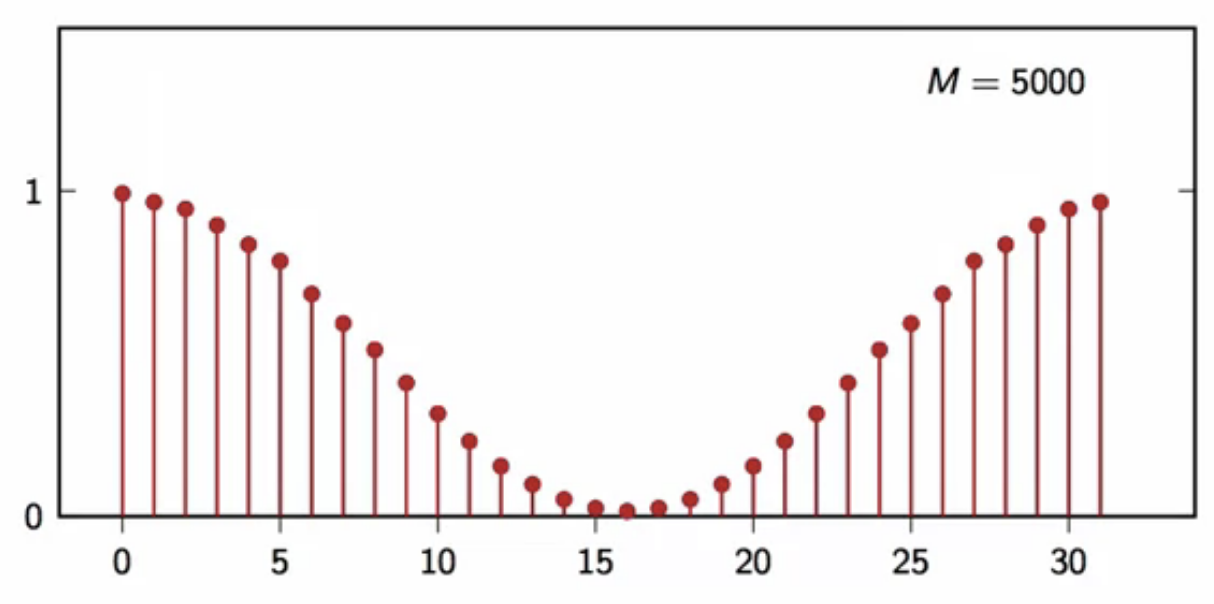
DFT-random-signal-avg

fig: moving average filtered output DFT average (M = 5000)

  • as the number of realizations used to compute the average increases, the shape converges
  • the shape it converges to is defined below

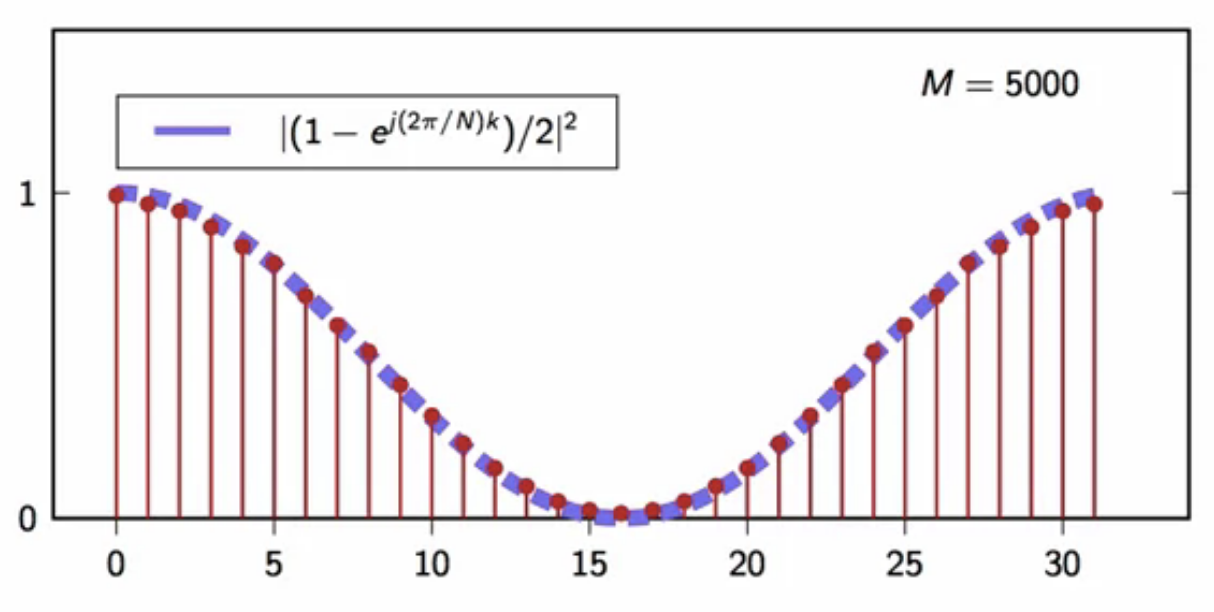
DFT-random-signal-avg

fig: moving average filtered output DFT average (M = 5000) - convergence shape

  • the power spectral density of the output is the product of the power spectral density of the input scaled by the squared magnitude of the filter frequency response \[ P_y[k] = P_x[k] \vert H[k] \vert^2 \text{, where } DFT{h[n] } ]
  • this result may be generalized beyond a finite set of samples
    • the world of infinite support stochastic processes

generalization

  • a stochastic process is characterized by its power spectral density (PSD)
  • it may be shown that PSD: \[ P_x(e^{j\omega}) = DTFT{ r_x[n] } ]
    • where:
      • ( r_x[n] = E[x[k]x[n+k]] ) is the autocorrelation of the process
  • for a filtered stochastic process ( y[n] = \mathcal{H} { x[n] } ), it is \[ P_y(e^{j\omega}) = \vert H(e^{j\omega}) \vert^2 P_x(e^{j\omega}) ]
  • this means that the filters designed for deterministic case still work in stochastic case
    • only in magnitude
  • the concept of phase is lost however, since the shape of a realization is not known in advance
  • only the power distribution across frequencies is known

noise

  • it’s everywhere
    • thermal noise
    • sum of extraneous interferences
    • quantization and numerical errors
  • we can model noise as a stochastic signal
    • since the noise source is not known
  • the most important noise is white noise

white noise

  • “white” indicates uncorrelated samples
  • so autocorrlation of noise signal is zero everywhere except zero - where it is the variance of the signal \[ r_w[n] = \sigma^2\delta[n] ]
  • has zero mean
  • the power spectral density is a constant
  • is equal to the variance of the process \[ P_w(e^{j\omega}) = \sigma^2 ]

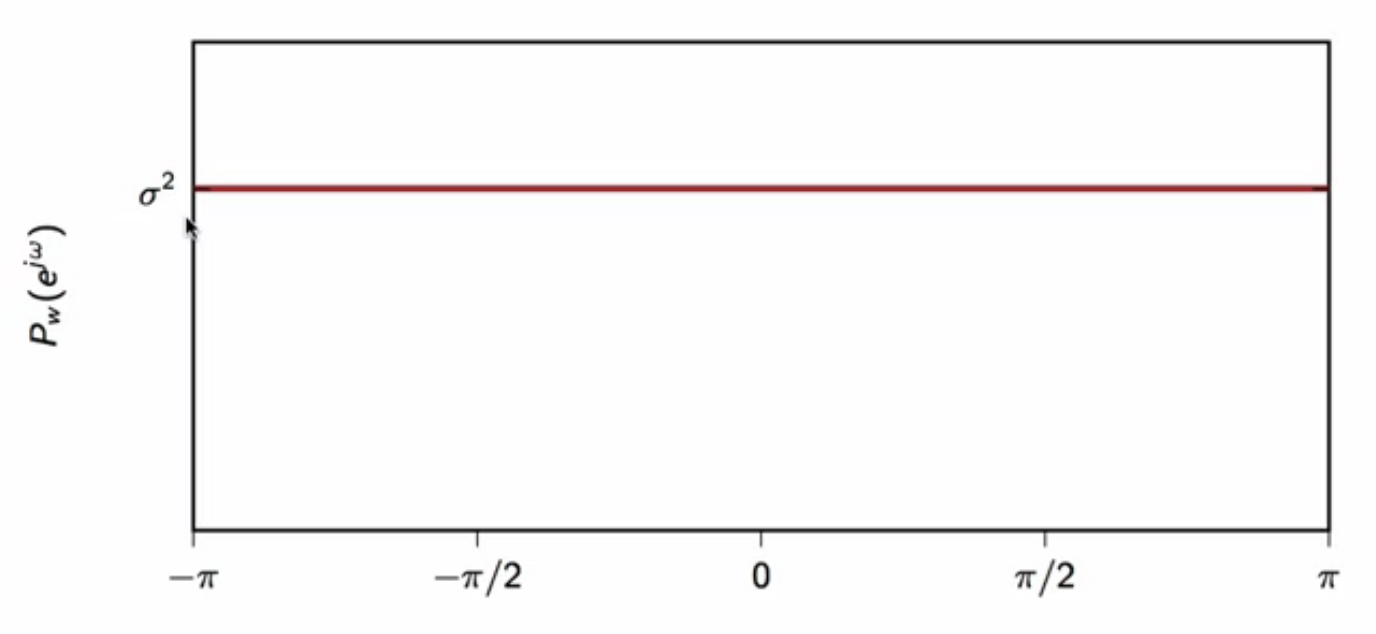
DFT-random-signal-avg

fig: power spectral density of white noise

  • the power spectral density of white noise is independent of the probability distribution of the signal samples
    • depends only on the variance
  • distribution is important to estimate bounds of the signal
    • in the time domain
  • very often, a gaussian distribution models the experimental data the best
    • represents many unknown additive sources of noise well
    • AWGN: additive white gaussian noise

quantization

  • this the second half of the story of dsp
  • digital devices can only deal with integers
    • (b) bits per sample
  • the range of a signal is to be mapped onto a finite set of values
    • this causes an irreversible loss of information
    • termed quantization noise
  • the finite set of values is the resolution of the system

quantizer

  • a quantizer takes in a discrete-time samples (x[n] \in \mathbb{C} )
  • it outputs integers ( \hat{x}[n] \in \mathbb{N} )
  • the output is said to be quantized version of the input discrete-time sequence

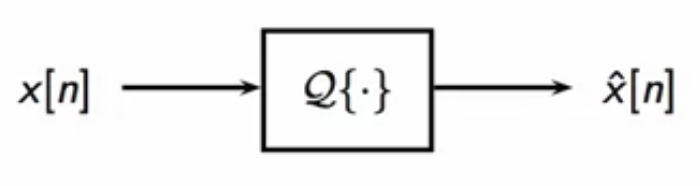
quantizer

fig: a quantizer block diagram representation

  • quantization considerations
    • storage budget
      • how many bits to allocate be sample
    • storage scheme
      • fixed point vs floating point
    • properties of input
      • range
      • probability distribution

scalar quantizer

  • it is the simplest quantizer
    • each sample is encoded individually
      • hence termed scalar
    • each sample is encoded independently
      • memoryless quantization
    • each sample is encoded using (R) bits
scaler quantizer operation
  • assume input signal bounded: ( A \leq x[n] \leq B ) for all (n)
    • each sample quantized over ( 2^R ) possible values
      • (R) bits per sample being used
      • in ( 2^R ) intervals
    • each interval associated to a quantization value quantizer fig: quantization into fixed intervals
example: (R = 2)
  • range (A-B) is divided into 4 intervals
  • ( i_k ) mark the boundaries of each interval
  • ( \hat{x}_k ) is the representative value of each interval
  • each interval is encoded into two bits
    • first interval: ( k = 00 )
    • second interval: ( k = 01 )
    • third interval: ( k = 10 )
    • fourth interval: ( k = 11 )
  • so the real value that represents an interval is associated with corresponding bit by the quantizer internally

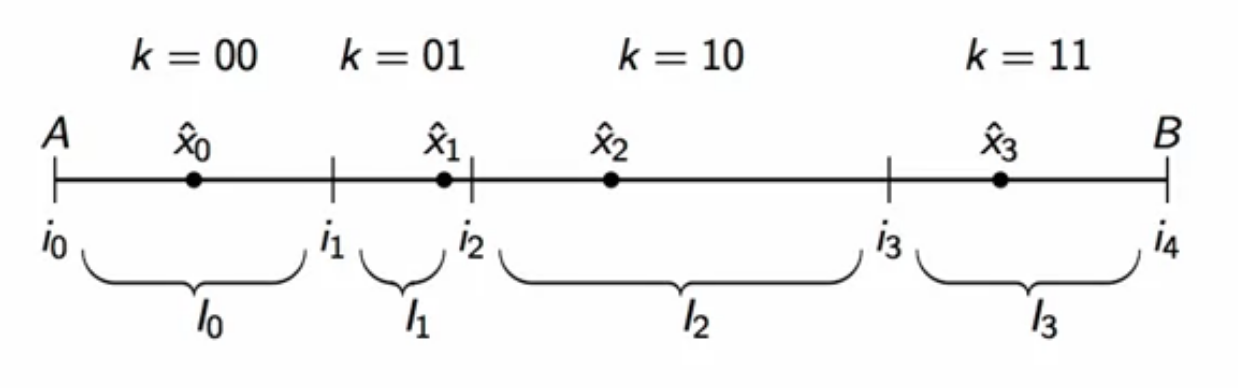
quantizer

fig: quantization into fixed intervals

  • optimization considerations;
    • interval boundaries ( i_k )
    • quantization values ( \hat{x}_k )

quantization error

  • quantization error is the difference between the representative value and the real value \[ \begin{align} e[n] & = \mathcal{Q}{ x[n] } - x[n]
    & = \hat{x}[n] - x[n]
    \end{align} ]
  • assumptions for preliminary analysis of error:
    • the input ( x[n] ) is modelled as a stochastic process
    • the error is modelled as white noise
      • error samples are uncorrelated
      • all error samples have the same distribution
  • assumptions are pretty drastic, but provide worst-case scenario insight
  • input statistical description is needed
  • assumptions for the internal structure of the quntizer:
    • uniform quantizaton
    • range is spilt into equal intervals
    • number of intervals: ( 2^R )
    • width of interval: ( \Delta = (B-A)2^{-R} )

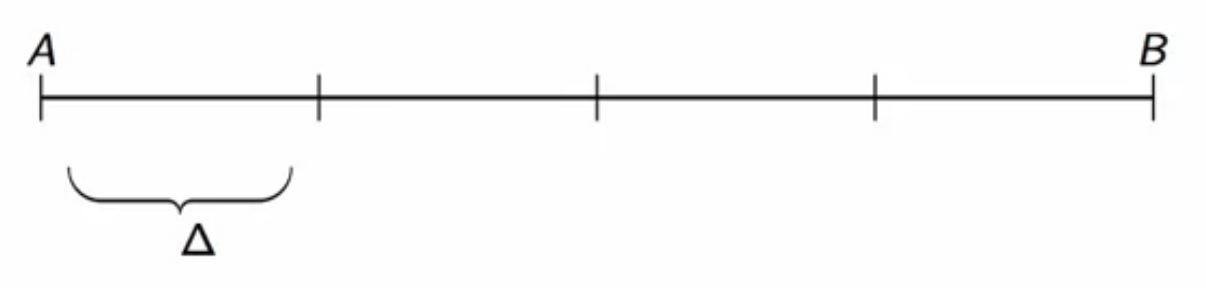
quantizer

fig: ( R=2 ) quantization intervals in range

  • mean-square-quantization-error is given by variance [ \begin{align} \sigma_e^2 & = E[\vert \mathcal{Q} { x[n] } - x[n] \vert^2 ] _
    & = \int{A}^{B} f_x(\tau)(\mathcal{Q} { \tau } - \tau )^2 d\tau _
    & = \sum{k=0}^{2^R - 1} \int_{I_k} f_x(\tau) (\hat{x}_k - \tau)^2 d\tau
    \end{align} ]
  • error depends on the probability distribution of the input
    • this needs to be known to evaluate quantization mse
  • continuing with more assumptions for this analysis…
  • the input is assumed to be uniformly distributed
    • input’s probability distribution function is a constant over the range (A-B)
      • with amplitude ( \frac{1}{B-A} )
  • with this assumption about the input, the mse therefore becomes [ \begin{align} \sigma_e^2 & = \sum_{k=0}^{2^R - 1} \int_{I_k} \frac{(\hat{x}_k - \tau)^2}{B-A} d\tau
    \end{align} ]
  • to find the optimal quantization point, this quantization mse is minimized [ \begin{align} \frac{ \partial \sigma_e^2 }{ \partial \hat{x_m} } & = \frac{ \partial }{ \partial \hat{x_m}} \sum_{ k = 0}^{ 2^R - 1} \int_{I_k} \frac{(\hat{x_k} - \tau)^2}{B-A} d\tau _
    & = \int{I_m} \frac{ 2( \hat{x_k} - \tau) }{ B - A } d\tau _
    & = \frac{ (\hat{x_m} - \tau)^2 }{B - A} \Bigg \vert{A + m \Delta }^{ A + m\Delta + \Delta}
    \end{align} ]
  • to minimize the error, set partial derivative of error to zero [ \begin{align} \frac{\partial \sigma_e^2}{\partial\hat{x_m}} = 0 & \text{ for } \hat{x_m} = A + m\Delta + \frac{\Delta}{2}
    \end{align} ]
  • so optimal quantization point for all intervals is the interval’s midpoint

quantizer characteristic

  • below is a 3 bits per sample quantizer characteristic

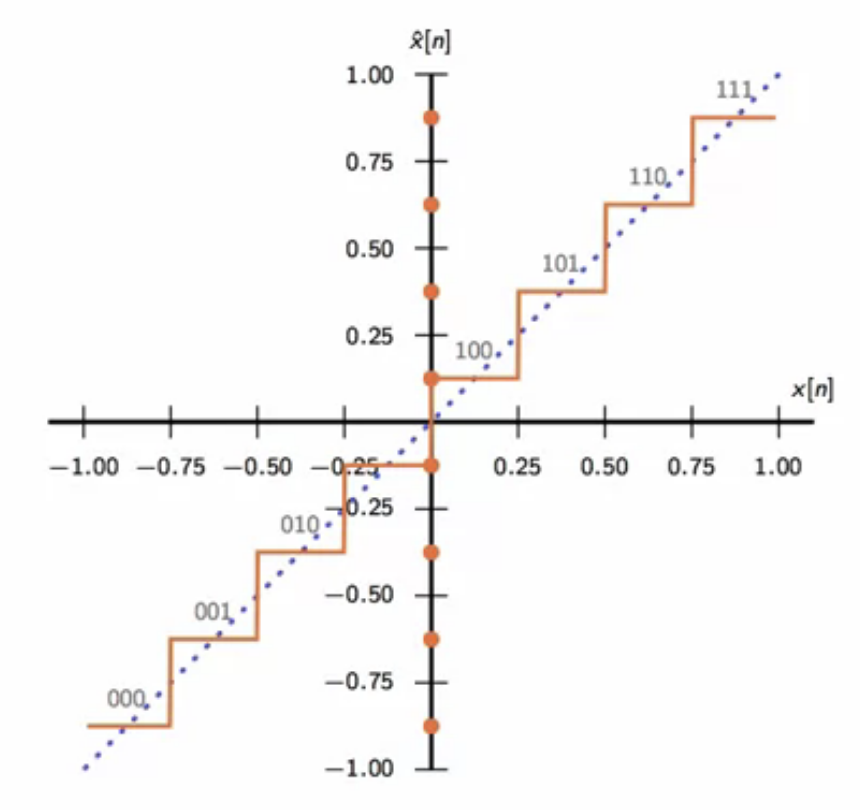
quantizer

fig: uniform 3-bit (R=3) quantizer characteristic

  • quantizer mse is [ \begin{align} \sigma_e^2 & = \sum_{k = 0}^{2^R - 1} \int_{A + k\Delta}^{A + k\Delta + \Delta} \frac{ (A + k \Delta + \frac{\Delta}{2} - \tau)^2}{B - A} d\tau
    & = 2^R \int_0^\Delta \frac{(\frac{\Delta}{2} - \tau)^2}{B-A} d\tau
    & = \frac{\Delta^2}{12}
    \end{align} ]

error analysis

  • error energy \[ \sigma_2^2 = \frac{\Delta^2}{12} ]
  • signal energy \[ \sigma_x^2 = \frac{(B-A)^2}{12} ]
  • signal to noise ratio \[ SNR = 2^{2R} ]
  • signal to noise ratio in (dB) [ SNR_{dB} = 10 \log_{10}^{2^{2R}} \approx 6R dB ]
6dB/bit rule of thumb
  • a CD has 16 bits/sample
    • max SNR = 96dB
  • a DVD has 24 bits/sample
    • max SNR = 144dB

references