[DSP] W08 - Modulation and Demodulation

signal preparation
modulation
demodulation
design example

the signal is prepared for transmission through the channel constraints
- this includes modulating the signal
on the receiver end, the signal is demodulated
- then is decoded to estimate the encoded information
- estimate because there is error in
  - the encoding
  - the decoding
  - also noise is added in the channel during propagation

signal preparation

the signal flows through the following
- signal in bitstream
- scrambler makes it random and white
  - power spectral density is constant across full specrtrum
- QAM mapper encodes bitstream to a complex valued symbol
  - resulting in $a [n]$
- upsampler fits encoded signal to channel bandwidth
  - K times more samples
- lowpass raised cosine remove the copies obtained after digital upsampling
  - cutoff frequency $\frac{π}{K}$

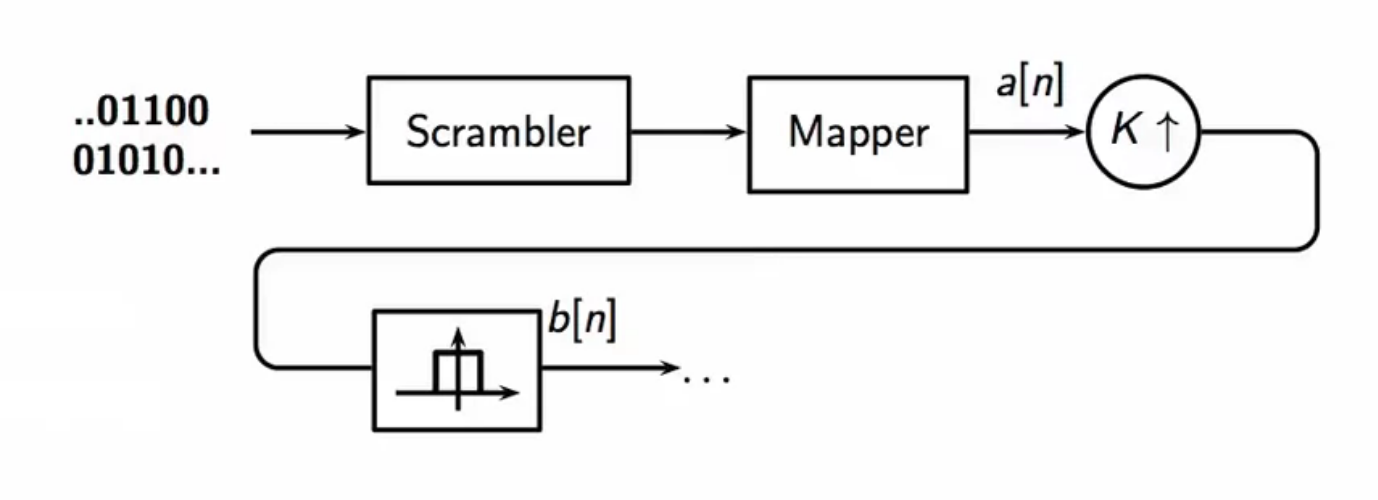
qam-transmitter

fig: QAM transmitter schematic

the signal thus obtained with a QAM decoder is $b [n]$ $b [n] = b_{r} [n] + j b_{i} [n]$
$b [n]$ is a complex-valued baseband signal
having been subjected upsampling, its bandwidth is meets the carrier constraint
- but does not sit in the bounds of the carrier’s bandwidth

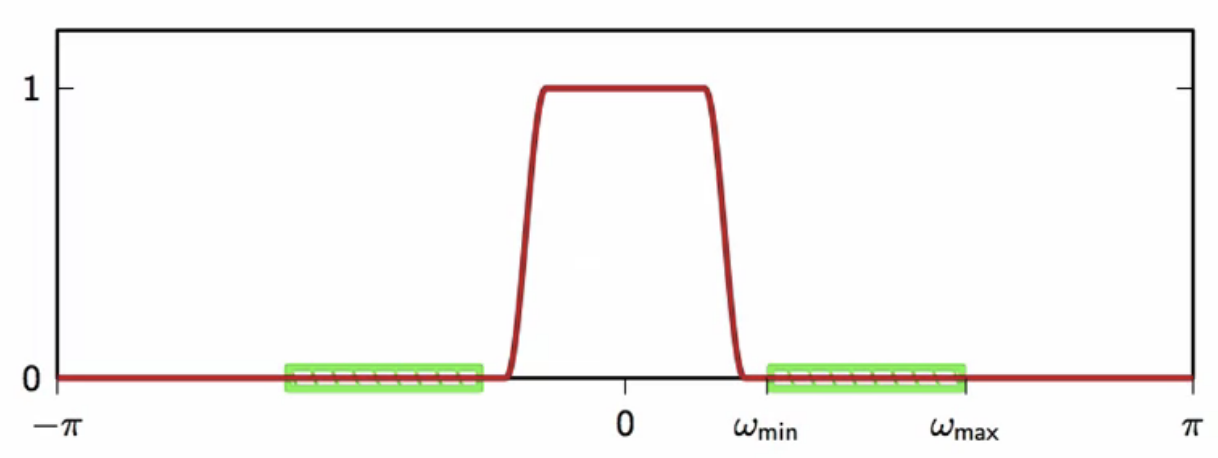
complex baseband signal

fig: carrier bandwidth availability (green) and $b [n]$ baseband (red)

modulation

modulation is the process of modifying the complex baseband that has the same size of the carrier bandwidth to sit exactly in the specified bandwidth
a complex baseband cannot be transmitted over a real physical channel
- to fully reconstruct the information at the other end
so the complex baseband has to be made real before transmission

discrete-time domain

let $ω_{c}$ be the center frequency of the channel bandwidth
then, the modulated, real baseband is obtained as follows $\begin{aligned} s [n] & = R e {b [n] e^{j ω n}} & = R e {(b_{r} [n] + j b_{i} [n]) (\cos ω_{c} n + j \sin ω_{c} n)} & = b_{r} [n] \cos ω_{c} n - b_{i} [n] \sin ω_{c} n \end{aligned}$
here,
- the real part of the complex baseband is modulated with a cosine and
  - in-phase component
- the imaginary part is modulated with a sine
  - quadrature component
- both are at the carrier bandwidth central frequency
- also, they are orthogonal to each other i.e. in quadrature
- this is the source of the name QAM used to encode with the complex number symbols
$s [n] \in N$
- is used at the receiver end to recover the complex baseband signal

complex discrete-frequency domain

before modulation
- real and imaginary component spectrums separated

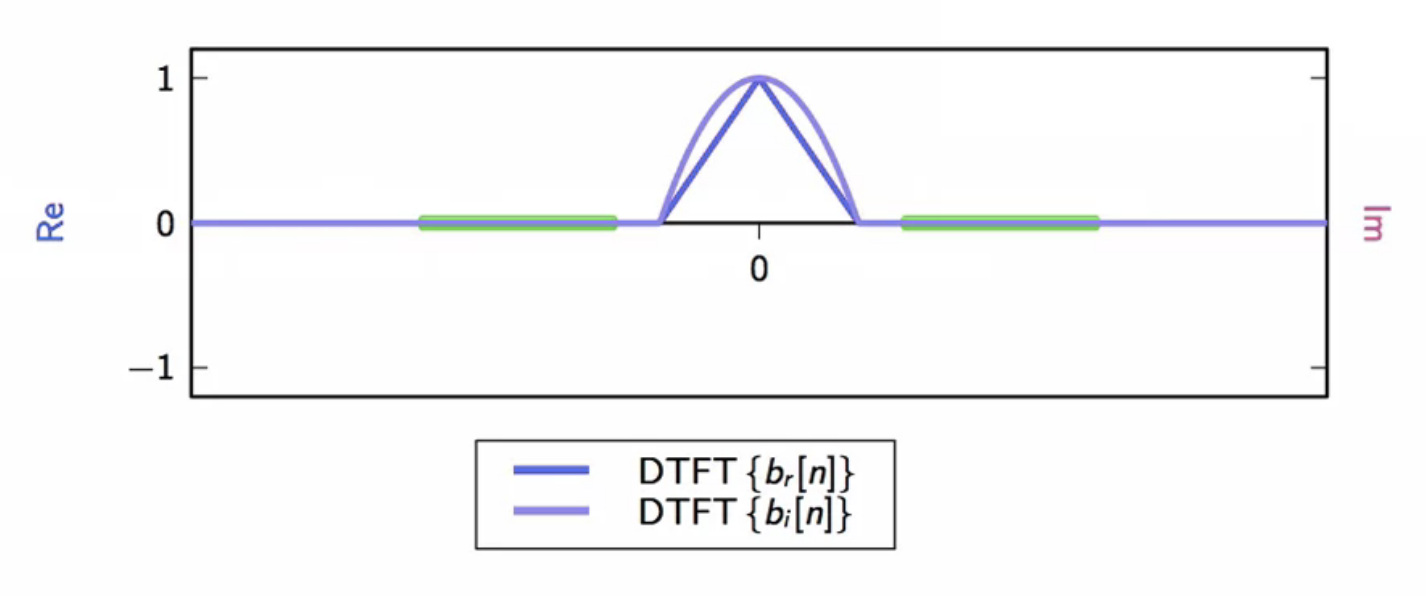
complex-baseband-signal-spectrum

fig: carrier bandwidth availability (green); $b [n]$ baseband real part (blue); $b [n]$ baseband imaginary part (pink)

after modulation
- real and imaginary modulated component spectrums separated
- the real part is symmetric
- the imaginary part is anti-symmetric

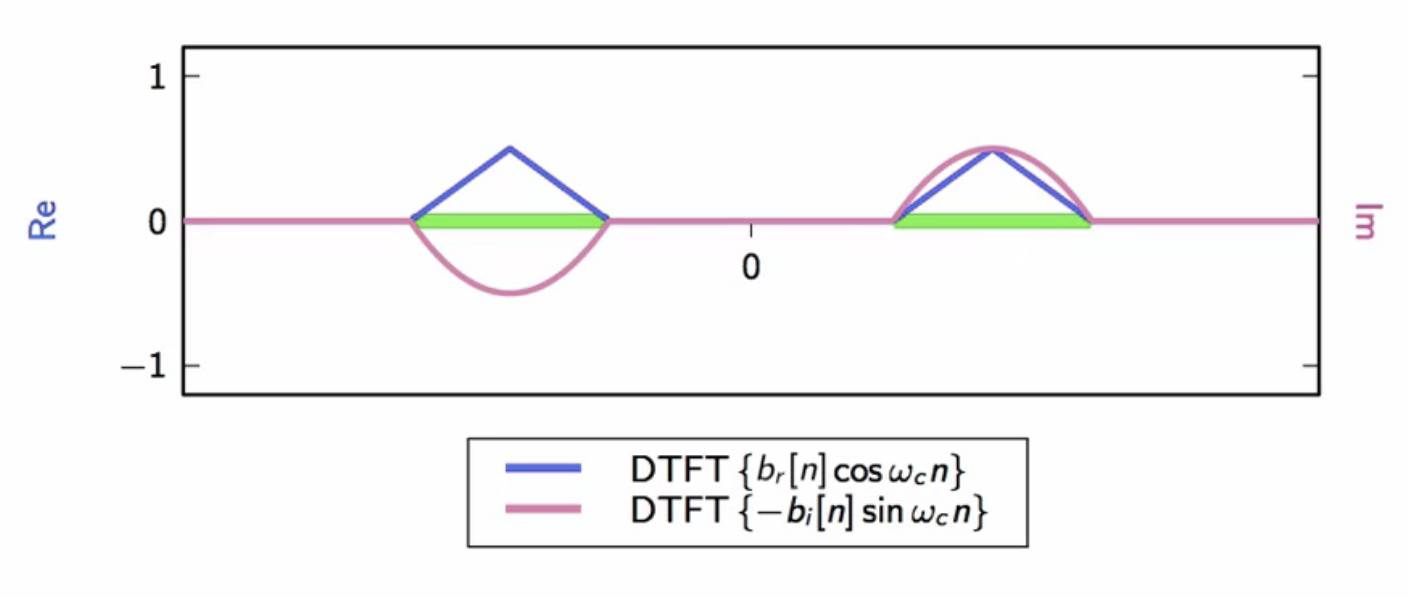
complex-baseband-signal-modulated

fig: carrier bandwidth availability (green); $b [n]$ baseband modulated real part (blue); $b [n]$ baseband modulated imaginary part (pink)

demodulation

demodulation is achieved by multiplying received signal by the carrier signal
in the QAM scenario, there are two carriers in the received signal
- one sine and one cosine

in-phase part extraction

begin with multiplying by cosine to extract the real part of the received baseband

$\begin{aligned} s [n] \cos ω_{c} n & = b_{n} [n] \cos^{2} ω_{c} n - b_{i} [n] \sin ω_{c} n \cos ω_{c} n & = b_{r} [n] \frac{1 + \cos 2 ω_{c} n}{2} - b_{i} [n] \frac{2 \sin 2 ω_{c} n}{2} & = \frac{1}{2} b_{r} [n] + \frac{1}{2} (b_{r} [n] \cos 2 ω_{c} n - b_{i} [n] \sin 2 ω_{c} n) \end{aligned}$

the frequency component reveals one half of the real part of the transmitted and received signal
- matched filter configuration: same raised cosine used at the transmitter is used at the receiver

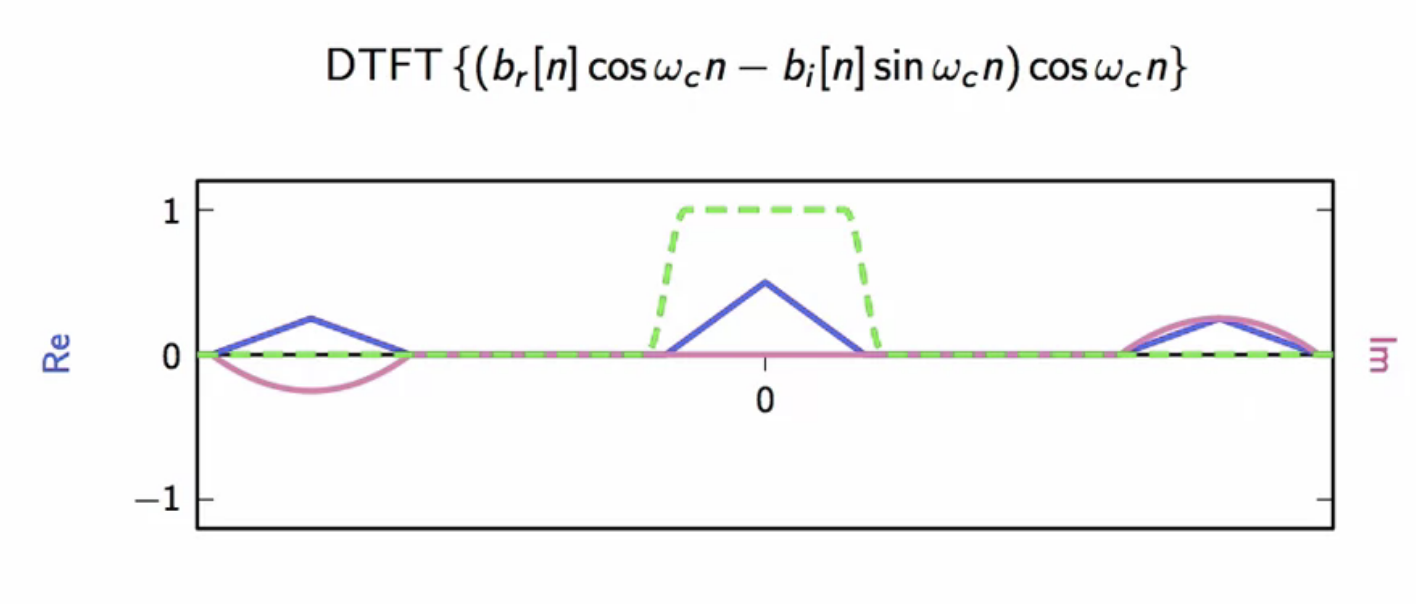
received-baseband-signal-demodulated

fig: frequency domain of signal after multiplying with cosine wave (blue); raised cosine lowpass applied (green)

the raised cosine will eliminate everything but the real part of the transmitted baseband

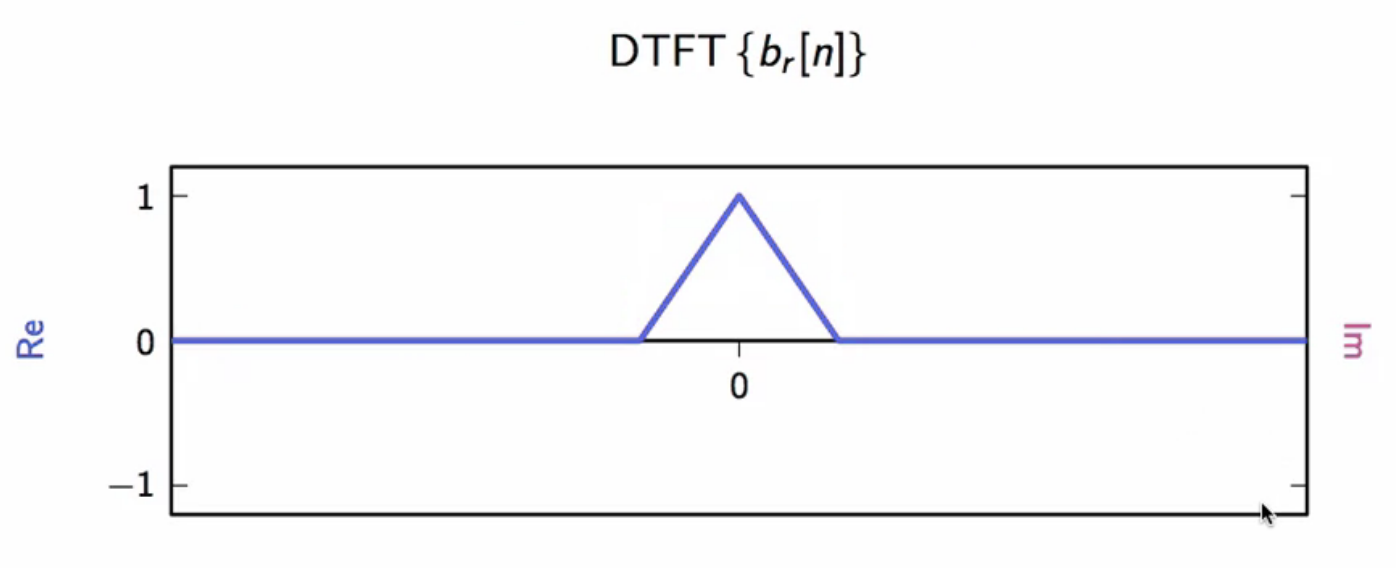
real-baseband-signal-extracted

fig: recovered real part of transmitted baseband

quadrature part extraction

multiply by sine to extract the imaginary part of the transmitted baseband

$\begin{aligned} s [n] \sin ω_{c} n & = b_{r} [n] \cos ω_{c} n - b_{i} [n] \sin^{2} ω_{c} n & = - \frac{1}{2} b_{i} [n] + \frac{1}{2} (b_{r} [n] \sin 2 ω_{c} n - b_{i} [n] \cos 2 ω_{c} n) \end{aligned}$

the frequency band looks similar to the demodulation of the in-phase part
the core signal is extracted with a raised cosine lowpass

design example

to be explored is a system that enables encoding and transmission of complex-valued sequence over a real-valued channel

QAM transmitter

the signal in a QAM transmitter is processed as follows:
- signal in bitstream
- scrambler makes it random and white
  - power spectral density is constant across full specrtrum
- QAM mapper encodes bitstream to a complex valued symbol
  - resulting in $a [n]$
- upsampler fits encoded signal to channel bandwidth
  - K times more samples
- lowpass raised cosine remove the copies obtained after digital upsampling
  - cutoff frequency $\frac{π}{K}$
- the filtered signal is multiplied with complex exponential whose frequency is the central frequency of carrier bandwidth
  - this results in a complex passband signal
- the real part of the complex baseband is extracted along with modulation
- this is sent to the DAC which propagates it into the channel

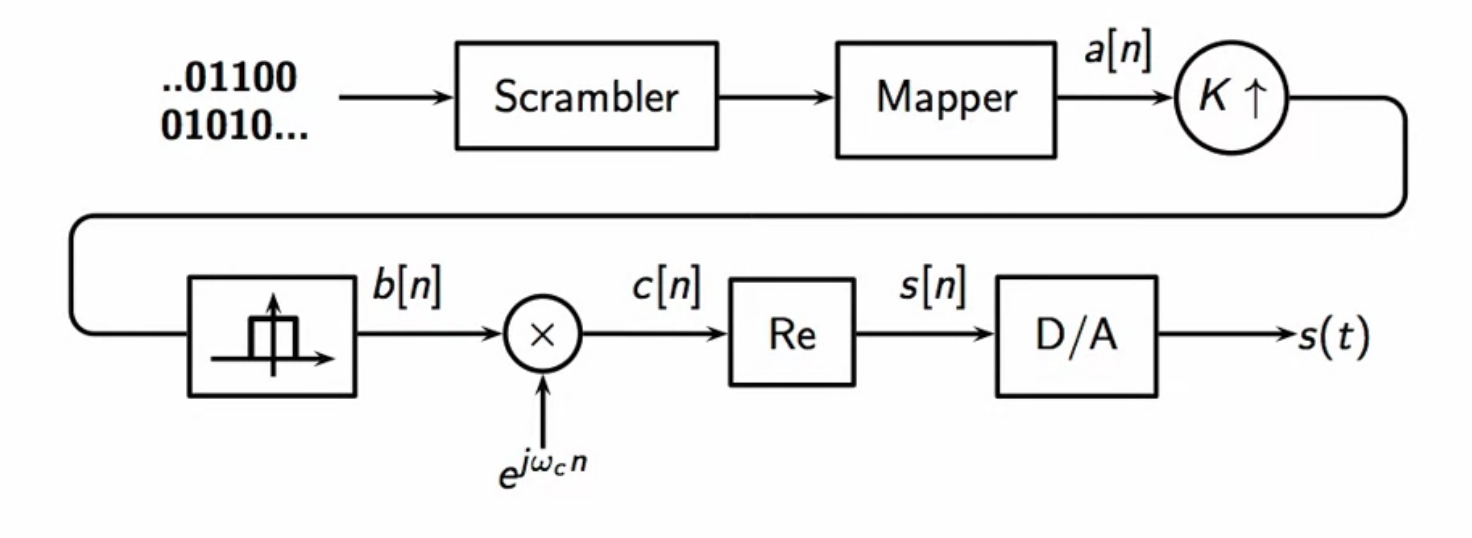
qam-transmitter

fig: QAM transmitter signal flow schematic

QAM receiver

goal of the receiver to obtain the original bitstream which is the core information that was transmitted
an ideal QAM receiver processes the received signal to retrieve that as follows:
- analog signal is received from the channel
- this analog signal is sampled with appropriate sampling rate
- signal is split into two parts to modulate with cosine and sine separately
  - cosine demod results in the real part
  - sine demod results in the imaginary part
- both demodulated signals go through their own lowpass filter
  - matched filter configuration: same lowpass used at the transmitter
- the imaginary component is multiplied with complex root to and summed with the real part to construct an estimate of the transmitted baseband
- this is then subjected to downsampling
- thus obtained complex symbol sequence is passed through a slicer
  - the bit chuck associated with the symbol is obtain so
- these chunks are assembled into a sequence and passed into a descrambler
  - this recovers the original bitstream

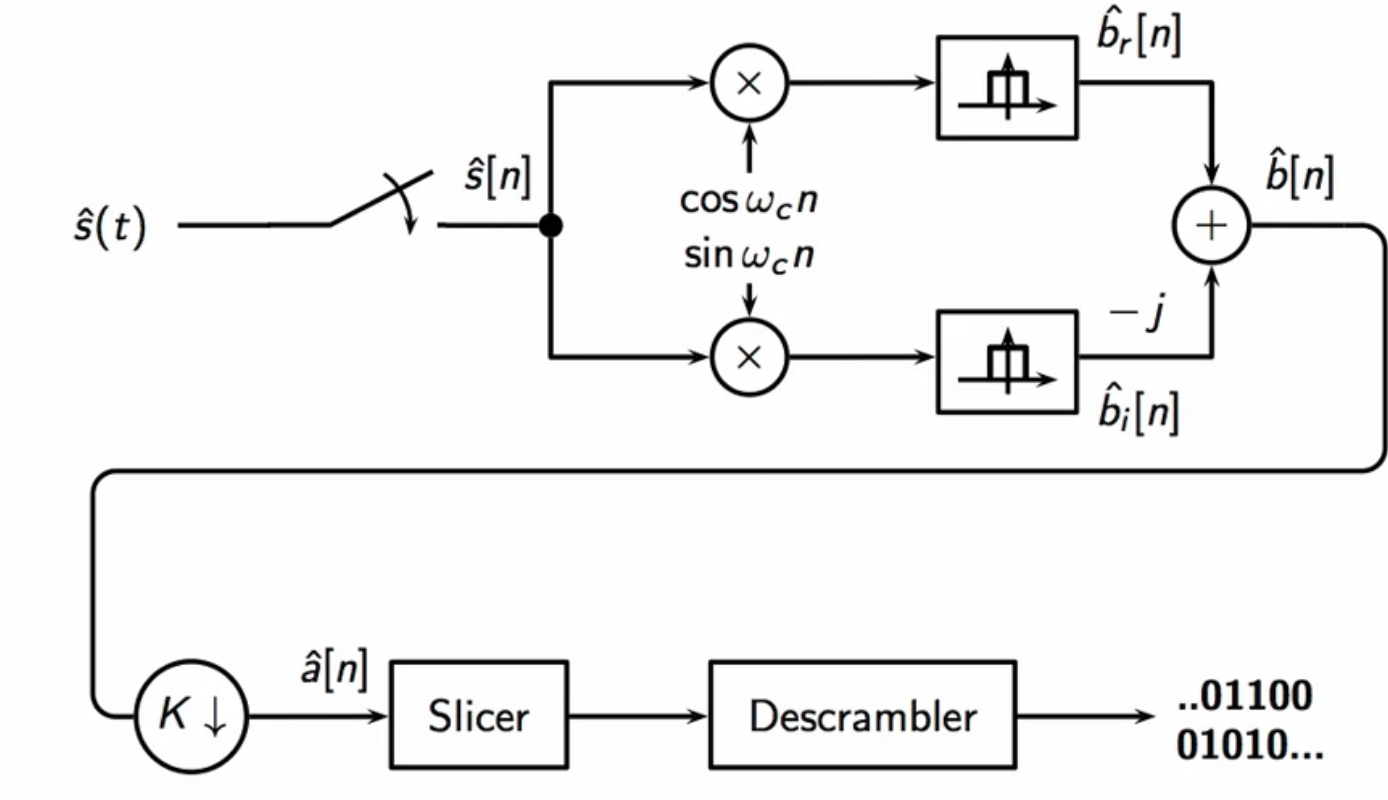
qam-receiver

fig: QAM receiver signal flow schematic

voiceband modem application

channel specifications

analog telephone channel
- $F_{m i n} = 450 H z; F_{m a x} = 2850 H z$
- usable bandwidth: $W = 2400 H z$
- center frequency: $F_{c} = 1650 H z$
- pick $F_{s} = 3 * 2400 = 7200 H z$
  - so K = 3
- $ω_{c} = 0.458 π$

bandwidth constraint

sampling theorem states that the sampling frequency is to be higher than twice the maximum frequency
- so atleast $F_{m a x} * 2 = 2850 H z = 5700 H z$
upsampling also has to be considered, so sampling frequency must also be an integer multiple of the channel bandwidth
- channel bandwidth $W = 2850 - 450 = 2400 H z$
- with center frequency $F_{c} = 1650 H z$
- if upsamling factor is chosen to be three, then $K = 3$
- so sampling frequency $F_{s} = 3 * W = 23 * 2400 = 7200 H z$
  - this satisfies the sampling theorem frequency criteria as well
- in the digital domain, $ω_{c} = 0.458 π$
  - this is the modulating frequency

power constraint

maximum SNR: $22 d B$
pick $P_{e r r} = 10^{- 6}$
using QAM, find M (number of bits per signal) $M = \log_{2} (1 - \frac{3}{2} \frac{10^{\frac{22}{10}}}{l n (10^{- 6})}) \approx 4.1865$
so pick M = 4 and use 16-point constellation
- 4 points in each quadrant
final data-rate is $W M = 4 * 2400 H z = 9600$ bits per second
- W: baud rate (bandwidth of the channel)

theoretical channel capacity

capacity formula based on signal bandwidth and SNR $C = W \log_{2} (1 + S N R)$
only gives upper bound on the amount of information that can be sent over the channel
doesn’t actually state how to build a communication system to meet this specification
for the previously designed scheme
- $C \approx 17500$ bps
- this hits half the channel capacity
the gap can be narrowed with encoding techniques
this topic needs a more thorough study of information theory

references

ecole

contents