[DSP] W08 - Receiver Design

contents

• receiver design
• delay compensation
• adaptive equalization
• adsl
  • channel propagation challenges
  • subchannel structure
  • discrete multitone modulation
  • ADSL schematic

---

• signal picks up noise while propagating in the channel
• it also get distorted as the channel acts as some sort of filter,
  • that is not necessary lowpass or linear-phase
• interference occurs as well

• there might be parts of the channel that might assumed to be usable and actually not

• the receiver has to deal with a copy of the transmitted signal
  • very far from the idealized version used in the math for designing the transmitter
• adaptive filtering techniques enable digital receivers to cope with the distortions and the noise introduced by the channel
  • topics: advanced signal processing classes
• this is an overview
  • your ADSL receiver for instance
  • allows high data rates

receiver design

• following is the sound made by a dial-up internet modem
  • when connecting to the internet

• for graphical analysis of this sound, refer to receiver schematic below

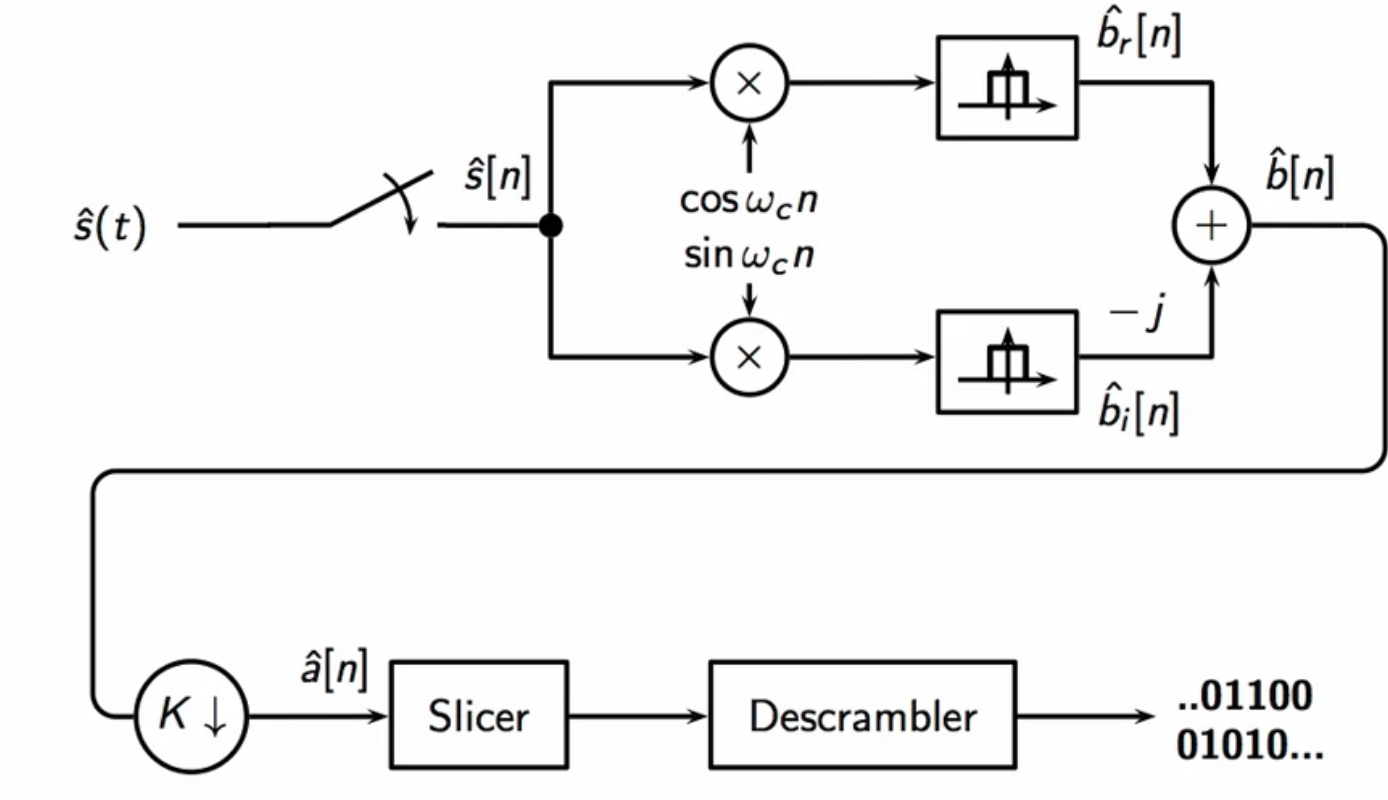
fig: QAM receiver signal flow schematic

• baseband complex samples $\hat{b}\left[n\right]$ are plotted on the complex plane
• if the input at the receiver is a signal $\hat{s}\left[n\right]=\cos \left(\right({\omega }_c+{\omega }_0\left)n\right)$
  • the obtained baseband for this is $\hat{b}\left[n\right]=e^{j{\omega }_{0}n}$
  • so they point on the unit circle on the argand plane
  • the angle between successive points will be ${\omega }_0$

pilot tones

• the receiver sends pilot tones
• pilot tones are simple sinusoids used to probe the channel
  • channel probing

• used to gauge the response at particular frequencies

• some components
  1. many sinusoids
     • which have abrupt phase changes
     • phase reversals are used as time markers
     • to estimate propagation delay of channel
  2. training sequence
     • known sequence is sent my transmitter
     • the receiver uses channel response to this known sequence to train an equalizer to offset channel effects
  3. handshake procedure between transmitter and receiver
     • just before core information transmission begins
     • low bitrate QAM transmission using only four points
       • 2 bits per symbol
       • parameters exchange of speed, constellation size etc
       • since only 4 points constellation,
         • so even in noisy conditions ensure vital information exchange
  4. data transmission proper

receiver function

• challenges faced at the receiver and measures taken to offset each challenge
  • interference
    • handshake and line probing
  • propagation delay
    • delay estimation
  • linear distortion
    • adaptive equalization
  • clock drifts between the receiver and the transmitter
    • timing recovery
    • advanced topic

main challenges

• challenge distortion

• time-varying discrepancies in clocks $T_s^{\prime }=T_s$

• the channel is approximated as a linear filter in the continuous-time domain to begin analysis
  • $D\left(j\omega \right)$: filter response
  • the filter is assumed to introduce all distortion and delays
• signal at receiver end: $\hat{s}\left(t\right)$
  • delayed and distorted version of transmitted signal
• clock of transmitter: $T_s$
• clock of receiver: $T_s^{\prime }$
  • no guarantee these two are synchronized

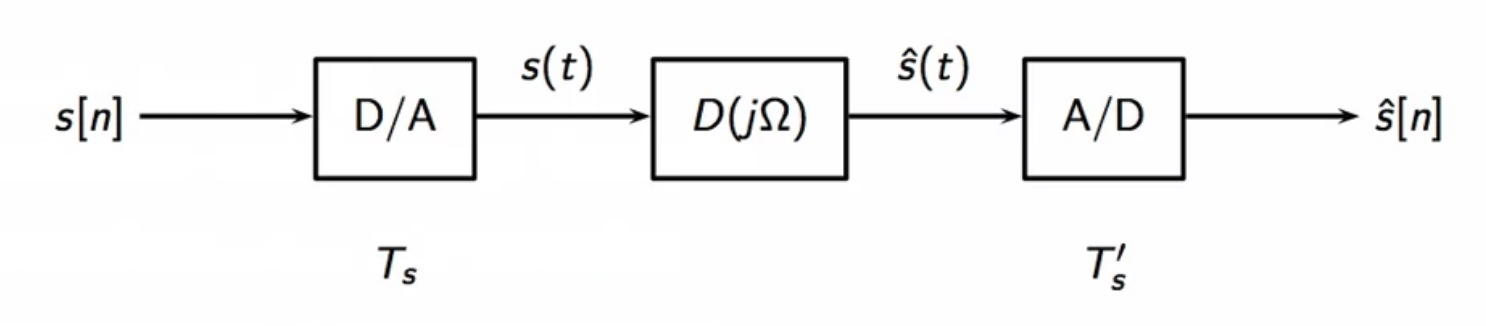
fig: DAC at transmitter and ADC at the receiver

---

delay compensation

• assuming the following are in sync
  • clock of transmitter: $T_s$
  • clock of receiver: $T_s^{\prime }$
• channel introduces a delay of $d$ seconds
  • channel is a simple delay block
  • $\hat{s}\left(t\right)=s(t-d)\to D\left(j\Omega \right)=e^{-j\Omega d}$
• we can write $d=(b+\tau )T_s$ with $b\in N$ and $\left|\tau \right|<\frac{1}{2}$
• $b$ is the bulk delay

• $\tau$ is the fractional delay

• bulk delay is simple to tackle
  • also called the integer delay
  • they are simply the delay that the channel adds to the signal
  • this does not sift the peaks of the data with respect to the sampling interval
• discontinuities in pilot tones help figure out bulk delay
  • impulses cannot be used as they are full band and get filtered out
• the fractional delay is more involved
  • it shifts the peaks with respect to the sampling intervals
  • interpolation is used to get the fractional delay compensation
• transmit $b\left[n\right]=e^{j{\omega }_{0}n}$
  • $s\left[n\right]=\cos \left(\right({\omega }_c+{\omega }_{)}\left)n\right)$
• receive $\hat{s}\left[n\right]=\cos \left(\right({\omega }_c+{\omega }_0\left)\right(n-b-\tau \left)\right)$
• after demodulation and bulk delay offset
  • $\hat{b}\left[n\right]=e^{j{\omega }_0(n-\tau )}$
• multiply by known frequency
  • $\hat{b}\left[n\right]e^{-j{\omega }_{0}n}=e^{-j{\omega }_0\tau }$
• after offsetting bulk delay
  • $\hat{s}\left[n\right]=s(n-\tau )T_s$
• subsample values need to be computed
• in theory, compensate with a sinc fractional delay
  • $h\left[n\right]=sinc(n=\tau )$
• in practice use lagrange approximation
  • practical application of lagrange polynomials
• lagrange approximation is around $n$
  • to compute $x(n+\tau )$ with $\left|\tau \right|<\frac{1}{2}$

$$\begin{array}{cccc}{x}_L(n;t)& =\sum _{k=-N}^{N}x[n-k]L_k^{\left(N\right)}\left(t\right)L_k^{\left(N\right)}\left(t\right)& =\prod _{i=-N;i\ne k}^n\frac{t-i}{k-i}\text{where}& =k=-N,\dots ,N\end{array}$$

• $x(n+\tau )\approx x_L(n;\tau )$
• so, in summary
  • estimate the delay $\tau$
  • compute the $2N+1$ lagrangian coefficients
  • filter with the resulting FIR

---

adaptive equalization

• measure to compensate for distortion
• let the channel distortion be $D\left(z\right)$
  • $E\left(z\right)$ is the equalizer compensation to offset channel distortion
• in theory $E\left(z\right)=1/D\left(z\right)$
• but $D\left(z\right)$ is not known

• $D\left(z\right)$ may change over time during transmission

• hence the equalization $E(z$ needs to adapt continuously
• following is the schematic of an adaptive equalizer

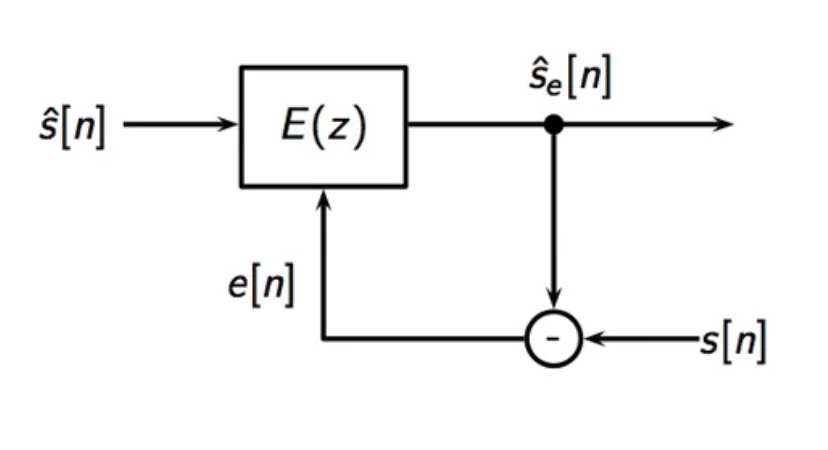
fig: core adaptive equalizer schematic

• the filter coefficient changes in time based on the error
  • obtained from the output with the transmitted signal
• the exact signal is sent by the transmitter
  • the receiver has the same copy to get the adaptive equalizer started
  • this is a bootstrapping technique
• there are some symbols that are common to both the transmitter and receiver together
  • this is called a training sequence
  • handshake 4 point QAM
  • the equalizer is initialized with this shared symbol set

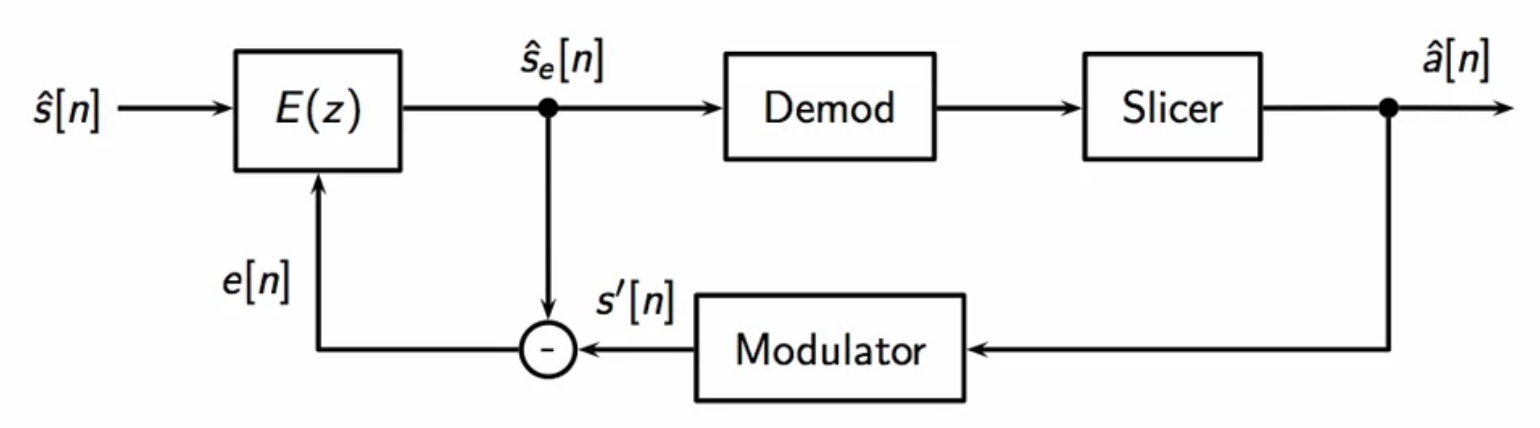
fig: adaptive equalizer schematic in the big picture

• this process of bootstrapping is not error free
  • but a generally good place to get started
• details of adaptive signal processing is an advanced topic
  • needs more research, reading and understanding

---

adsl

• ADSL: asymmetric digital subscriber line
• adsl receives signals on a copper wire channel
• DSLAM: digital subscriber line access multiplier

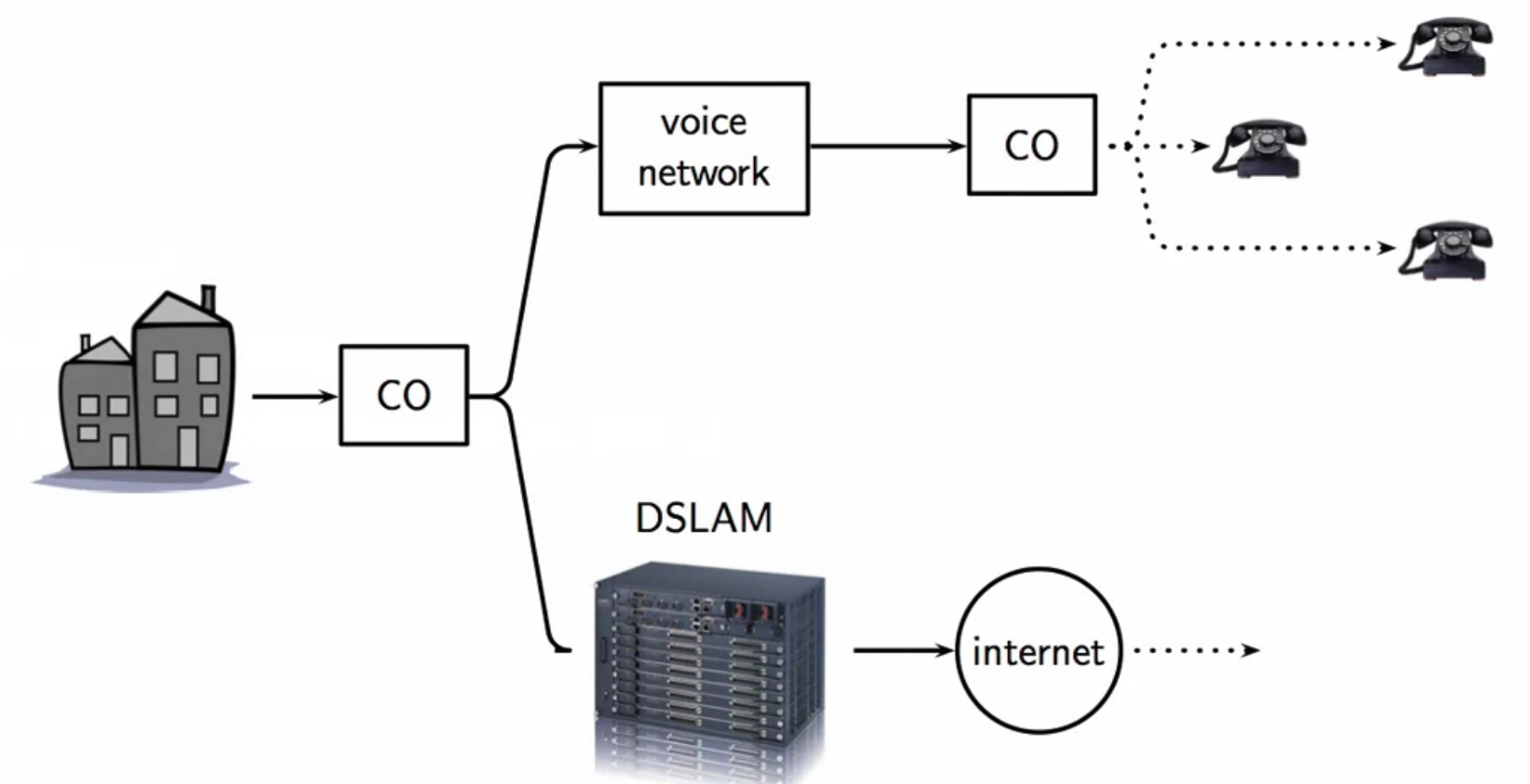
fig: telephone network overview

• last mile: copper wire connecting the home modem to the exchange (CO - central office)
• copper wire has a large bandwidth
• POTS: plain old telephone system
• the (A)symmetry in the bandwidth is the A of the ADSL

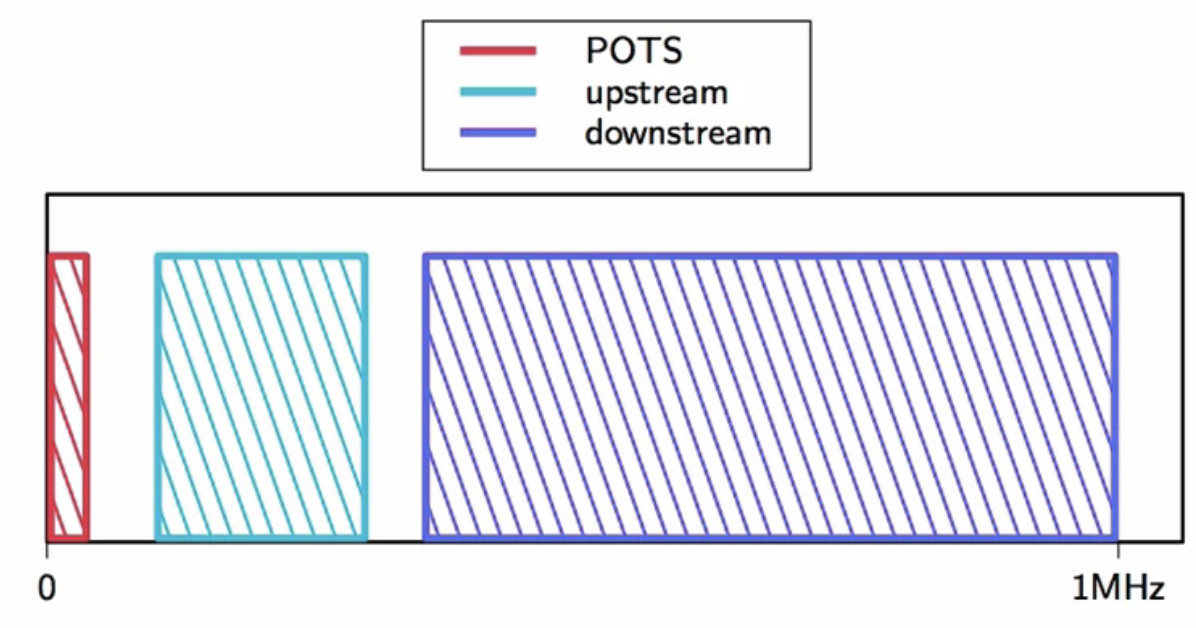
fig: adsl channel - copper wire bandwidth

channel propagation challenges

1. attenuation: the uneven curve across the bandwidth
   • physical wire imperfections
   • parasitic capacitance
2. electrical interference: large grey blog in a specific frequency region
   • running the vacuum for instance raises the noise floor of the copper channel
3. localized radio interference: the impulse at a specific frequency
   • ship-to-shore communications: 0 - 100 kHz
   • airplane communications: 100 - 500 kHz
   • AM radio band: 500 kHz +

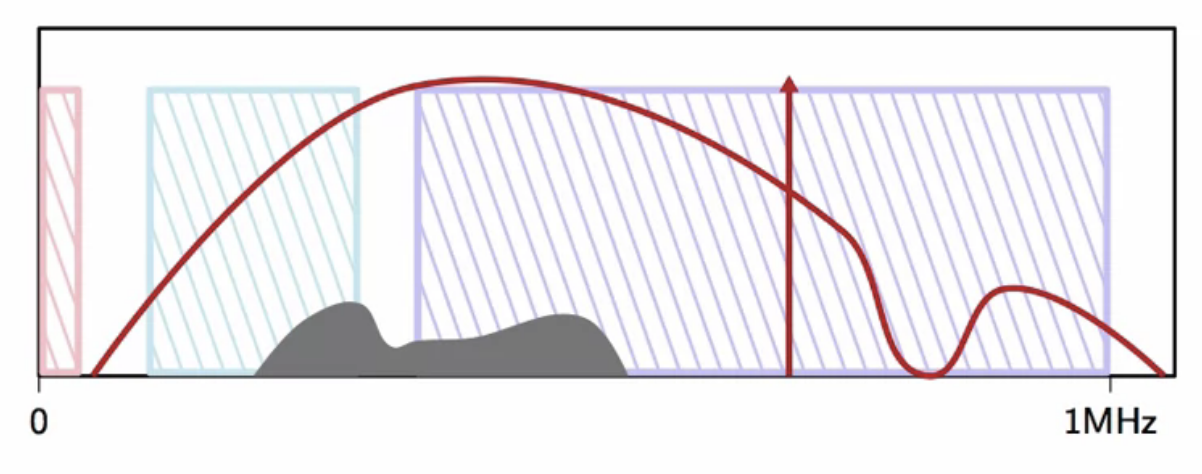
fig: adsl channel propagation challenges

• the channel is divided into independent sub-channels
• different channels are treated separately
  • localized treatment in the receiver across all bands
  • the cleanest channels are used to send maximum data

subchannel structure

• allocate N sub-channels over the total positive bandwidth
• equal sub-channel bandwidth $\frac{F_{max}}{N}$
• equally spaced sub-channels with center frequency $\frac{k{F}_{max}}{N}$
  • $k=0,\dots ,N-1$

digital design

• pick $F_s=2F_{max}$
  • $F_{max}$ is high now
• center frequency for each subchannel
  • ${\omega }_k-2\pi \frac{k{F}_{max}/N}{F_s}=\frac{2\pi }{2N}k$
• bandwidth of each sub-channel $\frac{2\pi }{2N}$
• to send symbols over a subchannel
  • upsampling factor $K\ge 2N$

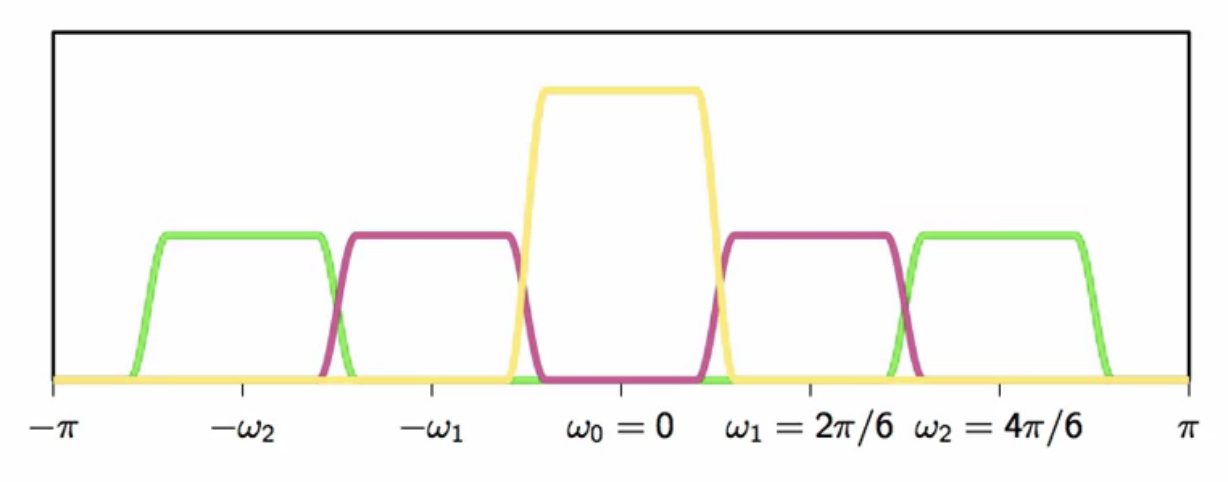
fig: subchannels of the adsl channel (N = 3)

• QAM modem is added on each channel
• decide on constellation size independently for each channel
  • clean channel gets high numbered constellation
  • noisy channel gets low numbered constellation
• noisy or forbidden sub-channels send zeros
• the structure of the communication scheme is sent to the receiver from the transmitter
  • part of handshake procedure
• classic modulation scheme is applied in each channel as per below schematic

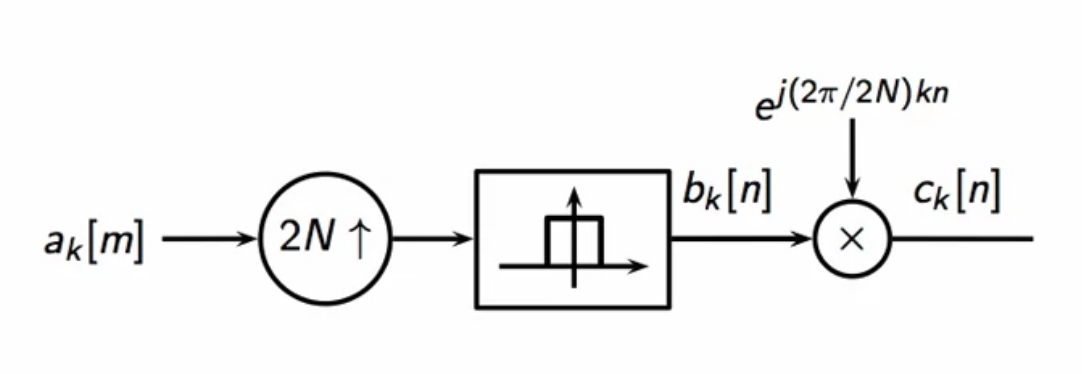
fig: modem on each sub-channel

• the receiver modem bank has several modems in parallel
• each channel has two unique attributes
  • frequency of modulation
  • mappers symbols series

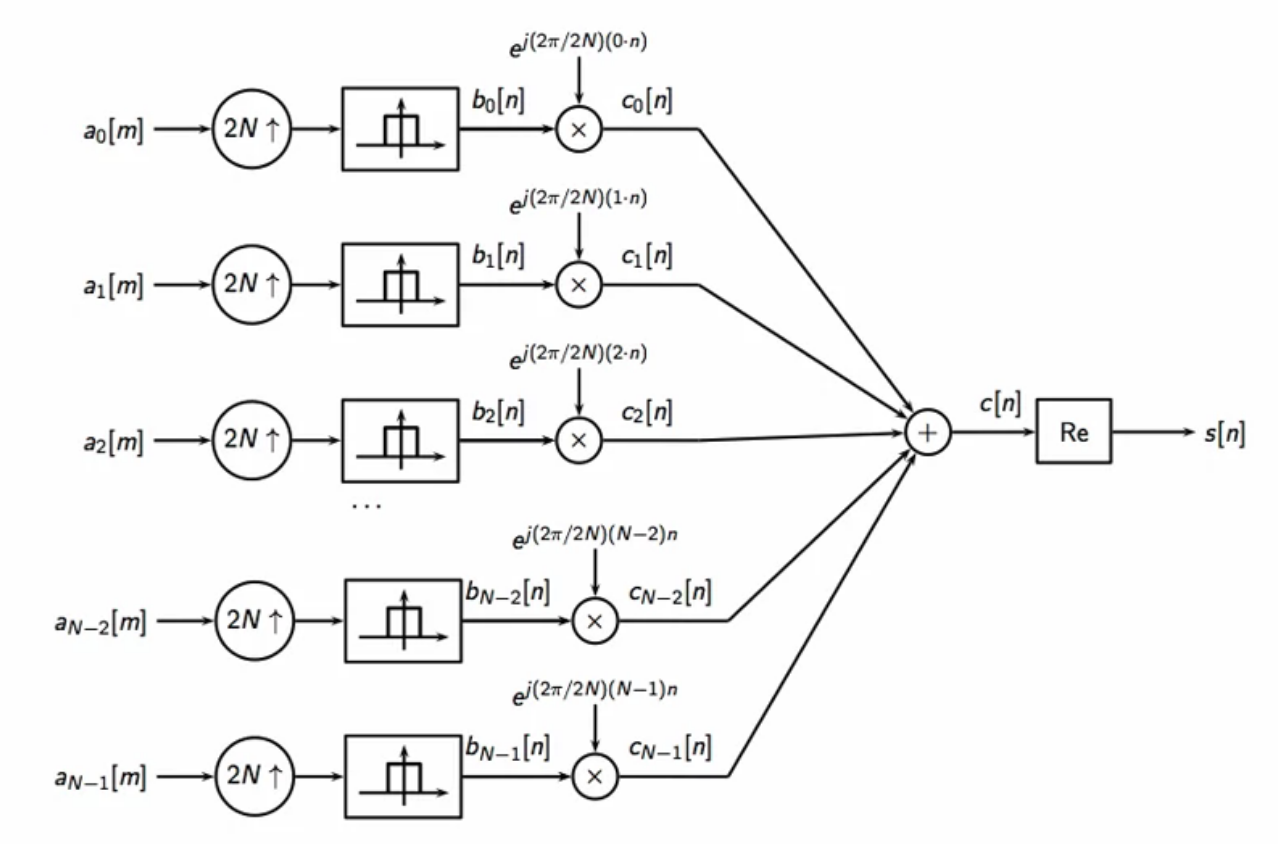
fig: modem bank

---

discrete multitone modulation

• the modem banks maybe seen as oscillators whose output is summed to obtain a signal
  • each oscillator is scaled with an amplitude
  • and phase offset
  • this bank is run for N samples to get the signal
  • these are constant through the generation

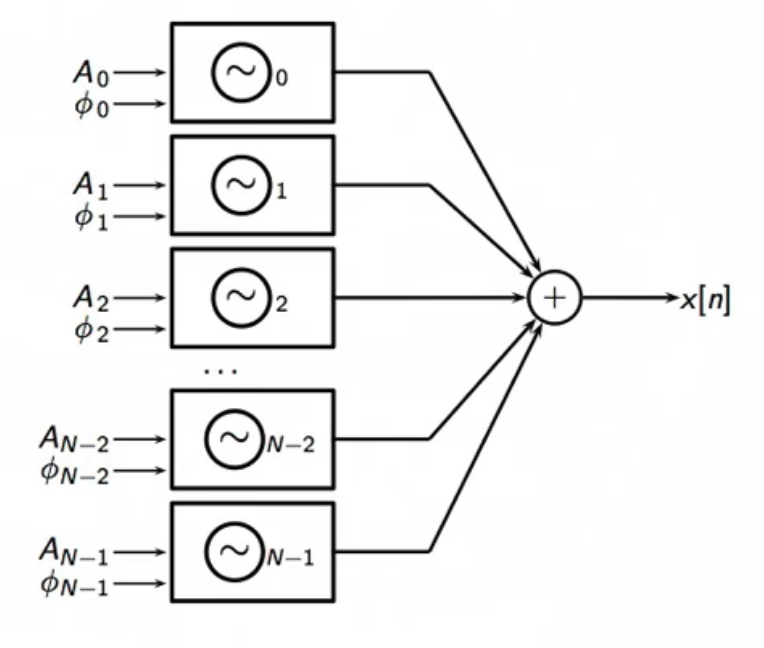
fig: oscillator bank paradigm for modem bank

• in the modem scenario, the amplitude and phase change at every sample
  • they embed the complex symbol sequence
• with the discrete multitone modulation, adsl may be implemented with a simple inverse FFT
  • provided that the symbols can be help constant during the whole upsampling event
  • the modem structure can be mapped to the inverse DFT structure if this is done
• the ADSL trick:
  • instead of using a god lowpass filter use a the 2N-tap interval indicator $$h\left[n\right]=(\begin{array}{cc}1& \text{for}0\le n\le 2N\\ 0& \text{otherwise}\end{array})$$

fig: modem on each sub-channel

• oscillator in the modulator runs freely
• with simplification, in each chunk of 2N samples, the symbol is kept constant

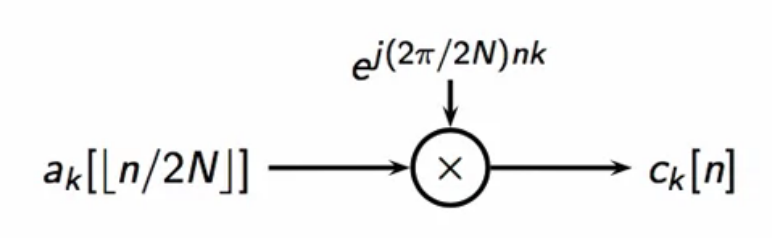
fig: simplification of subchannel modem

• aggregate bandpass signal is calculated by $$\begin{array}{cccc}c\left[n\right]& =\sum _{k=0}^{N-1}{a}_k[\lfloor \frac{n}{2N}\rfloor ]e^{j\frac{2\pi }{2N}nk}& =2N\ast IDF{T}_{2N}\left\{\right[a_0\left[m\right]a_1\left[m\right]\dots a_{N-1}\left[m\right]00\dots \left]\right\}\left[n\right]m& =\lfloor \frac{n}{2N}\rfloor \end{array}$$

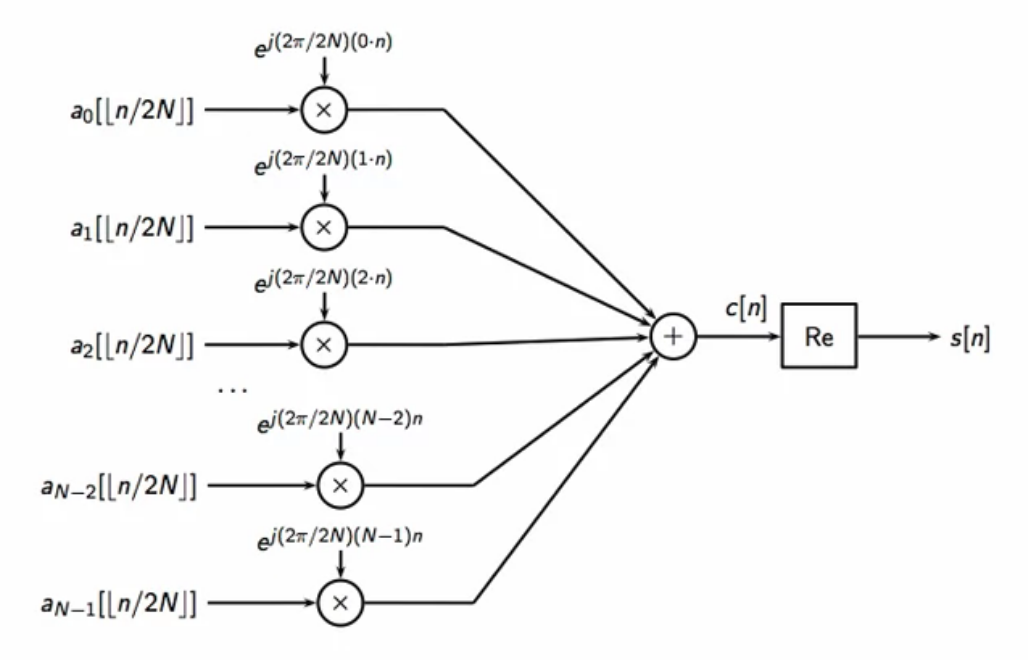
fig: simplified subchannels’ modem bank

• final goal: calculate $s\left[n\right]$ $$s\left[n\right]=Re\left\{c\right[n\left]\right\}=\frac{\left(c\right[n]+c^{\ast }[n\left]\right)}{2}$$

$$IDFT\left\{\right[x_0{x}_1\dots x_{N-2}{x}_{N-2}]{\}}^{\ast }=IDFT\{[x_0{x}_1\dots x_{N-2}{x}_{N-2}{]}^{\ast }\}$$

$$c\left[n\right]=2N\ast IDFT\left\{\right[a_0\left[m\right]a_1\left[m\right]\dots a_{N-1}\left[m\right]00\dots 0\left]\right\}\left[n\right]$$

• hence, since baseband always has read valued symbols

$$s\left[n\right]=N\ast IDFT\left\{\right[2a_0\left[m\right]a_1\left[m\right]\dots a_{N-1}\left[m\right]a_{N-1}^{\ast }\left[m\right]a_{N-2}^{\ast }\left[m\right]\dots a_1^{\ast }\left[m\right]\left]\right\}\left[n\right]$$

ADSL schematic

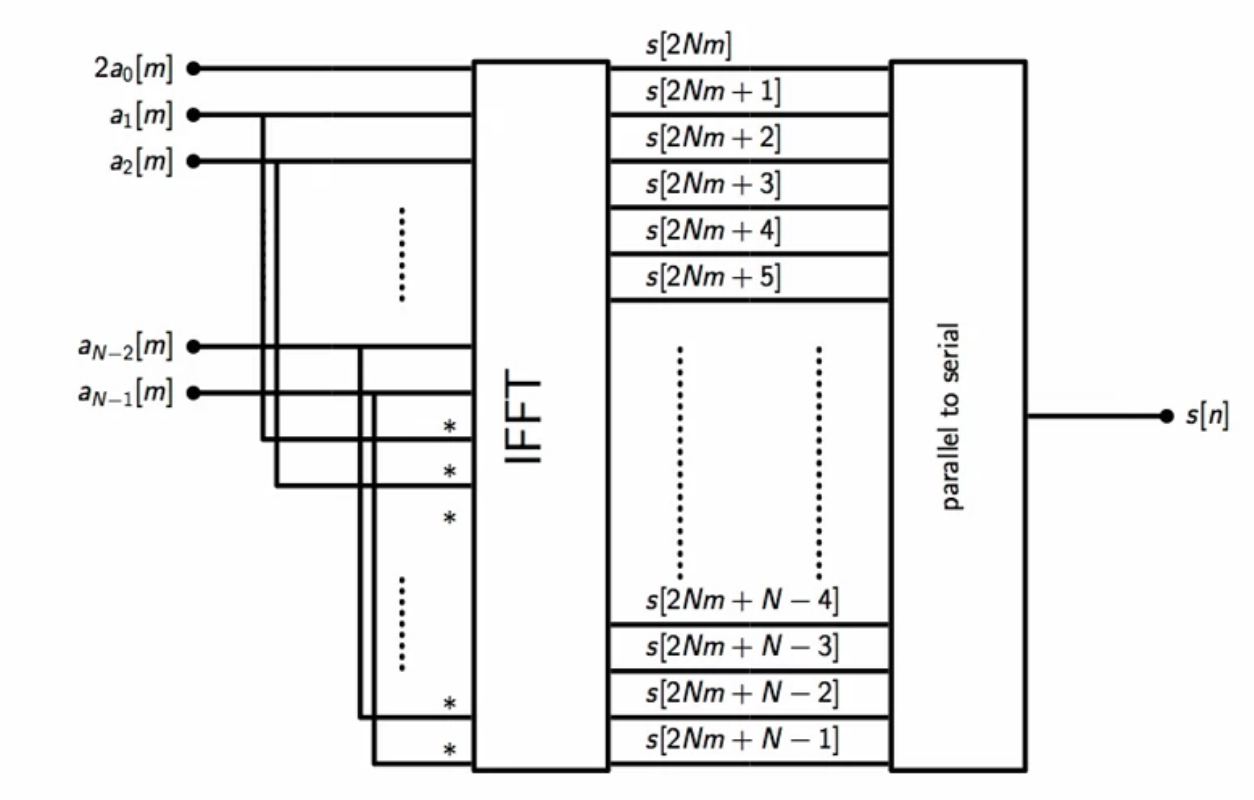
fig: simplified subchannels’ modem bank

ADSL specs

• $F_{max}=1104kHz$
• N = 256
• each QAM can send 0 - 15 bit per symbol
• forbidden channels 0 to 7
  • dedicated to voice
• channels 7 - 31: upstream data
• max theoretical throughput: 14.9 Mbps (downstream)

---

references

• ecole
• itu adsl specs
• itu v.34 modem specs