[QMSE] W01 - Classical Wave Equation

constructing the wave equation

• consider a series of masses on a string
  • at $\dots ,j-1,j,j+1,\dots$
  • spaced by $\Delta z$
• the pieces of strings connecting the masses have tension $T$
• the masses are at different heights from a reference horizontal
  • this also leads to a vertical force on the masses
  • because of the angle between the tensions in different pieces of string

• forces
  • $T\sin {\theta }_j$ pulls mass $j$ upwards
  • $T\sin {\theta }_{j-1}$ pulls mass $j$ downwards
  • the net upwards force on mass $j$ is
    • $F_j=T(\sin {\theta }_j-\sin {\theta }_{j-1})$
• for small angles
  • $\sin {\theta }_j\approx \frac{y_{j+1}-y_j}{\Delta z}$
  • $\sin {\theta }_{j-1}\approx \frac{y_j-y_{j-1}}{\Delta z}$
• using the small angles assumption in the force equation
  • $F_j=T(\sin {\theta }_j-\sin {\theta }_{j-1})$
  • $F_j\approx T[\frac{y_{j+1}-y_j}{\Delta z}-\left(\frac{y_j-y_{j-1}}{\Delta z}\right)]$
  • $F_j=T\left[\frac{y_{j+1}-2y+y_{j-1}}{\Delta z}\right]$
    • $\text{as}\Delta z\text{reaches infinitesimal limit}$
  • $F=T\left[\frac{y_{j+1}-2y_j-y_{j-1}}{\Delta z}\right]$
  • $F=T\Delta z\left[\frac{y_{j+1}-2y_j+y_{j-1}}{(\Delta z{)}^2}\right]$
  • $F=T\Delta z\frac{{\partial }^{2}y}{\partial z^2}$
• the resulting equations implies that force $F$ is proportional to the curvature of the string of masses
  • if all the masses are in a line, then there is no net force perpendicular to the line, either vertical or horizontal

linear density

• consider the mass string as a linear density
  • the amount of mass per unit length in the $z$ direction is $\rho$

• mass, $m$ is given by $m=\rho \Delta z$

• to get the force in terms of density, apply newton’s II law:
  • $F=m\frac{{\partial }^{2}y}{\partial t^2}=\rho \Delta z\frac{{\partial }^{2}y}{\partial t^2}$

putting the force from curvature and linear density force equations together

• $\rho \Delta z\frac{{\partial }^{2}y}{\partial t^2}=T\Delta z\frac{{\partial }^{2}y}{\partial z^2}$

• gives: $\rho \Delta z\frac{{\partial }^{2}y}{\partial t^2}=T\Delta z\frac{{\partial }^{2}y}{\partial z^2}$

• rearranging:
  • $\frac{{\partial }^{2}y}{\partial z^2}=\frac{\rho }{T}\frac{{\partial }^{2}y}{\partial t^2}$
• consider identity:
  • $v^2=\frac{T}{\rho }$
• this gives
• $\frac{{\partial }^{2}y}{\partial z^2}-\frac{1}{v^2}\frac{{\partial }^{2}y}{\partial t^2}=0$
• this is a wave equation for a wave with velocity $v=\sqrt{\frac{T}{\rho }}$
  • any function of the form $f(z-ct)$ is a solution of the wave equation
    • and is a wave moving to the right with velocity $c$
  • any function of the form $g(z+ct)$ is a solution of the wave equation
    • and is a wave moving to the left with velocity $c$

monochromatic waves

• waves oscillating at one specific (angular) frequency $\omega$

• temporal behavior of the form
  • $T\left(t\right)=exp\left(i\omega t\right),exp(-i\omega t),cos\left(\omega t\right),sin\left(\omega t\right)$
  • complex and real
  • or any combination of these, provided they comply with boundary conditions
• consider a monochromatic wave written as a product of variation in $z$ and a variation in $t$
  • $\varphi (z,t)=Z\left(z\right)T\left(t\right)$
  • double partial derivative w.r.t time gives
    • $\frac{{\partial }^2\varphi }{\partial t^2}=-{\omega }^2\varphi$

helmholtz wave equation

• plugging this into the simple harmonic equation
  • $\frac{d^{2}Z\left(z\right)}{d{z}^2}+k^{2}Z\left(z\right)=0$
    • where $k^2=\frac{{\omega }^2}{c^2}$
    • $c$: wave - velocity
  • this is called the helmholtz wave equation
    • simplest wave equation
    • used in CM for monochromatic wave

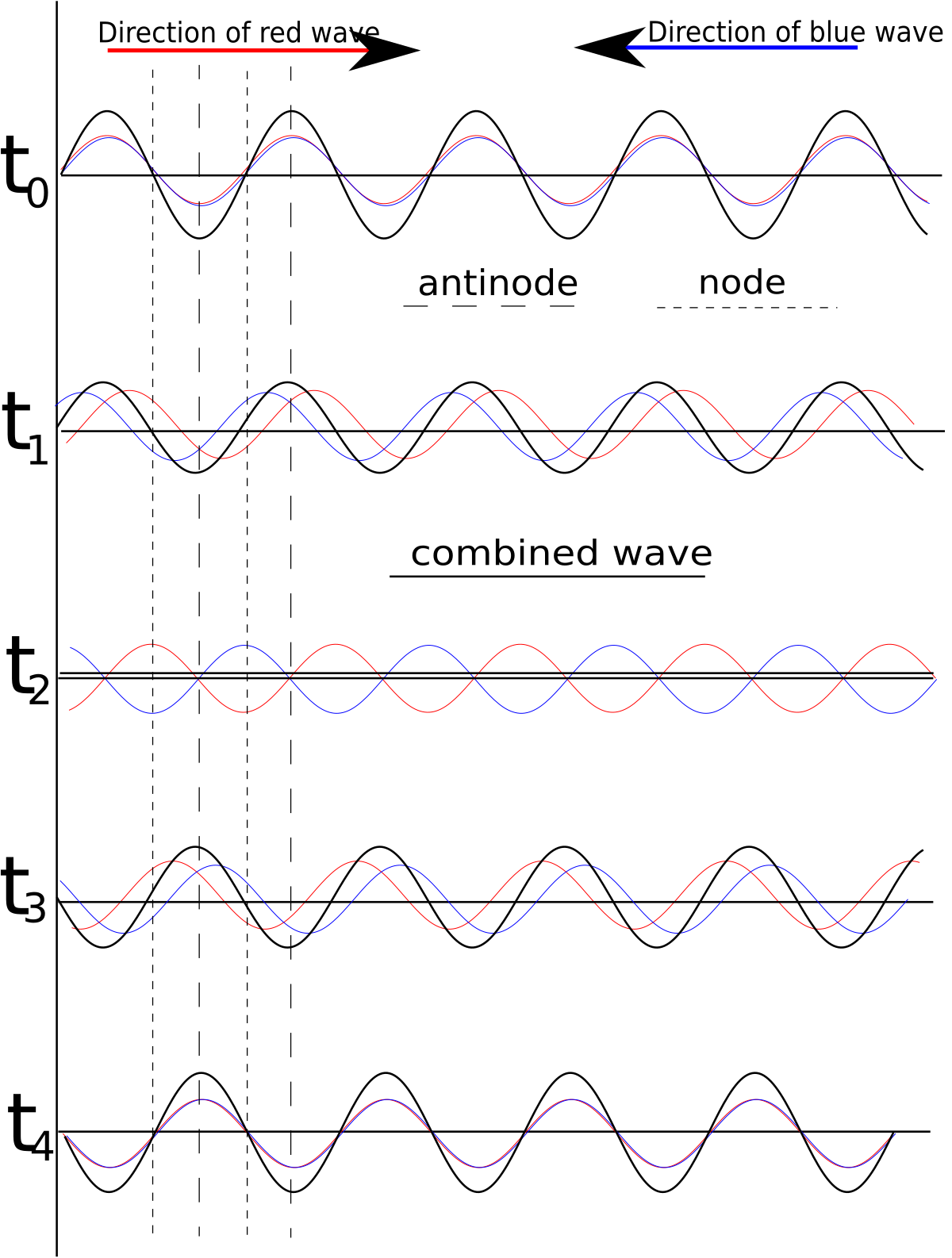
standing waves

• particularly important in QM

• needs matter that functions as a pair of walls

• standing waves are an equal combination of forward and backward waves
  • $\varphi (z,t)=sin(kz-\omega t)+\sin (kz+\omega t)$
• applying trigonometric identity
  • $\varphi (z,t)=2\cos \left(\omega t\right)\sin \left(kz\right)$, where $k=\frac{\omega }{c}$
• analogous to forces being in equilibrium
  • and net force begin equal to zero
• every point along the wave oscillates in time
  • but the spatial shape remains the same

example

• for a rope tied two two walls at distance L apart
  • $k=2\pi$
  • $\omega =\frac{2\pi c}{L}$